8  Análisis de estabilidad de sistemas

Nota

Para representar los diagramas de Bode utilizaremos el paquete Clasecontrol.jl. Para poder utilizarlo, es necesario añadir un registro a la lista de registros de Julia. Este paso solo hay que realizarlo una vez.

En el prompt de Julia, hay que cargar en primer lugar Pkg.jl:

using Pkg

A continuación, hay que añadir el registro:

pkg"registry add https://github.com/runjaj/Caronte"

Una vez realizada esta operación, no es necesario repetirla. El paquete Clasecontrol.jl se puede utilizar como cualquier otro paquete del registro oficial de Julia.

8.1 Definición de estabilidad. Ecuación característica

Un sistema dinámico es estable si para cualquier entrada acotada se obtiene una salida acotada, independientemente de cuál fuese su estado inicial.

La inestabilidad de los sistemas es la mayor limitación a la hora de realizar la sintonía del controlador.

Tal como se ha visto en los temas anteriores la respuesta de bucle cerrado para un sistema de control generalizado es:

\[y = \frac{G_c G_p G_f}{1 + G_c G_p G_f G_m} y_{sp} + \frac{G_d}{1 + G_c G_p G_f G_m} d \tag{8.1}\]

Normalmente, la estabilidad o inestabilidad de un sistema es intrínseca al mismo, independientemente de la entrada. Es un problema del sistema.

Para estudiar la estabilidad de la respuesta es necesario realizar la transformada inversa de Laplace para obtener la respuesta en tiempo real. Para ello hay que descomponer \(y(s)\) en fracciones simples. Para realizar esta descomposición se deben encontrar las raíces de la ecuación característica (\(1 + G_c G_p G_f G_m = 0\)). La ecuación característica es el denominador de las funciones de transferencia tanto del problema de la regulación o de la carga como del servocontrol (Figura 8.1), es decir, es 1 más el producto de las funciones de transferencia del lazo de retroalimentación (\(G_{OL}\)).

Figura 8.1: Diferentes objetivos de control, eliminación de perturbaciones o cambios en la carga (servomecanismo) y adaptación a nuevas condiciones o cambios en la consigna.

Las raíces de la ecuación característica son \(\alpha_i\), \(i = 1, \ldots, n\). Por tanto, una vez realizada la descomposición en fracciones simples:

\[y (s) = \frac{y_0}{s} + \frac{y_1}{s - \alpha_1} + \frac{y_2}{s - \alpha_2} + \ldots + \frac{y_n}{s - \alpha_n}\]

Tras realizar la transformada inversa de Laplace se obtiene la función en tiempo real:

\[y (t) = y_0 + y_1 \mathrm{e}^{\alpha_1 t} + y_2 \mathrm{e}^{\alpha_2 t} + \ldots + y_n \mathrm{e}^{\alpha_n t}\]

donde:

\[\alpha_i \in \mathbb{C}, \forall i\]

Es decir, todas las raíces de la ecuación característica son números complejos. Por tanto, para todo \(i\):

\[\alpha = \beta + \mathrm{i}\gamma \Rightarrow \mathrm{e}^{\alpha t} = \mathrm{e}^{\beta t} (\cos \gamma t + \mathrm{i}\sin \gamma t)\]

El valor de \(\gamma\) no influye en la salida del sistema desde el punto de vista de la estabilidad, ya que tanto el seno como el coseno son funciones acotadas. Solo cambia la frecuencia de la respuesta.

En cambio, si \(\beta\) es positivo, aparece un problema de estabilidad, porque la respuesta aumentaría constantemente con el tiempo. Por tanto, para que la salida del sistema sea estable todas las partes reales de las raíces de la ecuación característica deben ser negativas, deben estar situadas en el semiplano real negativo. En el caso de que alguna no lo fuese:

\[\lim_{t \to \infty} y (t) = \infty\]

Con esta información es posible diseñar técnicas que permitan seleccionar las constantes del controlador garantizando la estabilidad del sistema.

8.2 Método de Routh-Hurvitz

El método de Routh-Hurvitz permite comprobar de una manera rápida y sencilla si alguna de las partes reales de las raíces de la ecuación característica es positiva sin necesidad de tener que encontrar las raíces.

Operando la ecuación característica se obtiene:

\[1 + G_c G_p G_f G_m \equiv a_0 s^n + a_1 s^{n - 1} + \ldots + a_{n - 1} s + a_n = 0\]

donde \(a_0\) debe ser positivo.

El criterio de estabilidad de Routh-Hurvitz es:

1. Condición necesaria pero no suficiente: Todos los coeficientes \(a_0, a_1, \ldots, a_n\) de la ecuación característica deben ser positivos para que el sistema sea estable. Si alguno de los coeficientes es negativo, al menos una de las raíces tendrá la parte real positiva.

2. Condición necesaria y suficiente: Se construye la matriz de Routh:

   \[\begin{array}{c|ccccc} 1 & a_0 & a_2 & a_4 & a_6 & \ldots\\ 2 & a_1 & a_3 & a_5 & a_7 & \ldots\\ 3 & A_1 & A_2 & A_3 & \ldots & \\ 4 & B_1 & B_2 & B_3 & \ldots & \\ 5 & C_1 & C_2 & C_3 & \ldots & \\ \vdots & \vdots & \vdots & \vdots & & \\ n + 1 & W_1 & W_2 & & & \end{array}\]

   donde:

   \[\begin{aligned} & A_1 = \frac{a_1 a_2 - a_0 a_3}{a_1},\ A_2 = \frac{a_1 a_4 - a_0 a_5}{a_1},\ A_3 = \frac{a_1 a_6 - a_0 a_7}{a_1},\ \ldots & \\ & B_1 = \frac{A_1 a_3 - a_1 A_2}{A_1},\ B_2 = \frac{A_1 a_5 - a_1 A_3}{A_1},\ \ldots & \\ & C_1 = \frac{B_1 A_2 - A_1 B_2}{B_1},\ C_2 = \frac{B_1 A_3 - A_1 B_3}{B_1},\ \ldots & \\ & \vdots & \end{aligned}\]

   El sistema será estable si todos los términos de la primera columna de la matriz (\(a_0, a_1, A_1, B_1, C_1, \ldots, W_1\)) son positivos. Si alguno de estos elementos es negativo el sistema será inestable. Por cada cambio de signo habrá una raíz con la parte real positiva.

El criterio de estabilidad de Routh presenta algunas limitaciones. No puede tratar sistemas con retrasos (tiempos muertos) o no lineales. Solo da información de si un sistema es estable o inestable, no da información de si un sistema estable está cerca o lejos de la inestabilidad. Otra limitación es la necesidad de tener que expresar la ecuación característica como un polinomio en \(s\), esto puede ser bastante complicado en sistemas complejos.

Para encontrar qué valores de las constantes del controlador están situadas en el límite de estabilidad se debe resolver la siguiente ecuación:

\[W_1 s^2 + W_2 = 0\]

De esta manera se puede determinar un par de raíces de la ecuación característica con la parte real nula, es decir, situadas sobre el eje imaginario. Lógicamente, \(W_1\) y \(W_2\) dependen de los parámetros del controlador.

Ejemplo

En el problema 8.2 se utiliza el criterio de Routh-Hurvitz para demostrar la estabilidad de un lazo de control por retroalimentación.

8.3 Método del lugar de las raíces

Representando las raíces de la ecuación característica en el plano complejo es posible deducir el comportamiento de un sistema según su posición:

Figura 8.2: Situación en el plano complejo de diferentes raíces de la ecuación característica: a) Respuesta sobreamortiguada o críticamente amortiguada, b) límite de estabilidad y c) sistema inestable.

1. Si todas las raíces están en el semiplano negativo de \(s\), el sistema es estable

2. Si todas las raíces se encuentran en el eje real negativo (las raíces son números reales), el sistema está sobreamortiguado o críticamente amortiguado

3. Cuanto más alejadas del origen de coordenadas estén las raíces situadas en el eje negativo, más rápida será la dinámica del sistema (menor será la constante de tiempo)

4. Las raíces más cercanas al eje imaginario dominarán la dinámica de la respuesta mientras que aquellas que estén más alejadas dejarán de influir en la respuesta rápidamente

5. Cuanto más alejadas se encuentren las raíces conjugadas del eje real, más subamortiguado estará el sistema

Con esta información es posible plantear una técnica para estudiar la dinámica de un sistema a partir de su ecuación característica. Esta técnica es el lugar de las raíces, se basa en representar las raíces de la ecuación característica variando la ganancia del controlador entre cero e infinito. La abscisa es la parte real de las raíces y la ordenada es la parte compleja.

Representar las raíces de la ecuación característica para un sistema de primer o segundo orden es sencillo, ya que se pueden obtener ecuaciones analíticas que relacionan la posición de las raíces con la ganancia del controlador. Para sistemas de orden superior es más complejo, como consecuencia se han desarrollado métodos gráficos y métodos numéricos para facilitar esta tarea.

Ejemplo

En la primera parte del Problema 8.10 se estudia la estabilidad de un bucle de control mediante la localización de las raíces de la ecuación característica.

Frecuentemente, la función de transferencia de lazo abierto generalizada (\(G_c G_f G_p G_m\)) se puede escribir como un producto de ganancias \(K\) por una fracción de polinomios \(z(s)\) y \(p(s)\). Buscando los ceros de cada uno de estos polinomios, se puede escribir:

\[G_c G_f G_p G_m = K \frac{z (s)}{p (s)} = K \frac{(s - z_1) (s - z_2) \ldots (s - z_m)}{(s - p_1) (s - p_2) \ldots (s - p_n)}\]

donde \(z_i\) son los zeros y \(p_i\) son los polos de la función de lazo abierto (\(G_c G_f G_p G_m\)).

Para representar las raíces de la ecuación característica según la ganancia del controlador se pueden utilizar las siguientes reglas:

1. La representación de las raíces empieza (\(K_c = 0\)) en los polos de la función de transferencia de lazo abierto (\(G_c G_f G_p G_m\))

2. La curva finaliza (\(K_c = \infty\)) en los ceros de \(G_c G_f G_p G_m\). Si hay más polos que ceros, la curva tiende a infinito

3. El número de curvas es igual al orden del sistema y al de polos de \(G_c G_f G_p G_m\)

4. Las partes complejas de la curva siempre aparecen como complejos conjugados

5. El ángulo de las asíntotas de las curvas es igual a \(\frac{\pm180^{\circ}}{n - m}\) donde \(n\) es el número de polos de la función de transferencia de lazo abierto y \(m\) es el número de ceros

8.4 Análisis armónico de sistemas lineales. Diagramas de Bode

Esta técnica de análisis de estabilidad es completamente diferente a la de los dos apartados anteriores. También se la conoce como análisis de frecuencia.

Se basa en que cuando se introduce una señal sinusoidal en un sistema lineal se obtiene, tras un periodo transitorio, una respuesta sinusoidal de la misma frecuencia pero de amplitud diferente y desfasada. El análisis armónico estudia el desfase y la razón de amplitudes entre la entrada y la salida. Para un sistema de control por retroalimentación la razón de amplitudes (RA) nunca debe ser mayor de 1, ya que entonces se amplificaría la señal y el sistema se volvería inestable al retroalimentar la salida. El estudio del desfase es importante, ya que de cierta manera se puede considerar que da los mismos problemas que un retraso.

Para un sistema de primer orden con una entrada sinusoidal la razón de amplitudes será:

\[\mathrm{RA} = \frac{K_p}{\sqrt{1 + \omega^2 \tau_p^2}}\]

como se puede deducir a partir de la Ecuación 4.5.

Debido a la importancia de conocer RA se ha desarrollado una técnica matemática para determinarlo a partir de la función de transferencia sin necesidad de tener que obtener la respuesta del sistema en tiempo real.

Hay que sustituir \(s\) por \(\mathrm{i}\omega\), ya que se trata de un número complejo, para poder expresar la función de transferencia como un número complejo del tipo \(x + \mathrm{i}y\):

\[G (\mathrm{i}\omega) = \frac{K_p}{\tau_p \mathrm{i}\omega + 1} = \frac{K_p}{1 + \tau_p^2 \omega^2} + \mathrm{i}\left( - \frac{K_p \tau_p \omega}{1 + w^2 \tau_p^2} \right)\]

Para eliminar separar la parte real de la compleja, eliminar el número complejo \(\mathrm{i}\) del denominador, ha sido necesario multiplicar y dividir por el conjugado del denominador.

Figura 8.3: Representación del número complejo \(W\) en el plano complejo.

Cualquier número complejo \(W\) puede ser expresado, además de la manera habitual \(x + \mathrm{i}y\), como un módulo \(r\) y un argumento \(\varphi\):

\[\begin{aligned} W = x + \mathrm{i} y &= r (\cos \varphi + \mathrm{i}\sin \varphi) = r \mathrm{e}^{\mathrm{i}\varphi} \\ |W| = r &= \sqrt{x^2 + y^2} \\ \varphi &= \mathrm{atan} \left( \frac{y}{x} \right) \end{aligned}\]

Por tanto, la función de transferencia se puede expresar en función de \(r\) y \(\varphi\) como:

\[G (\mathrm{i}\omega) = \frac{K_p}{\sqrt{1 + \omega^2 \tau_p^2}} \mathrm{e}^{\mathrm{i}\varphi}\]

donde \(\frac{K_p}{\sqrt{1 + \omega^2 \tau_p^2}}\) es la razón de amplitudes y \(\varphi\) es el desfase. De esta manera se logra obtener el desfase y la razón de amplitudes sin tener que obtener la respuesta en tiempo real para una entrada sinusoidal de amplitud \(M\) y frecuencia angular \(\omega\).

En general, sea un sistema de orden \(n\) con la siguiente función de transferencia:

\[G (s) = \frac{Q (s)}{P (s)}\]

donde \(Q (s)\) y \(P (s)\) son polinomios de orden \(m\) y \(n\) respectivamente y \(m < n\). Se puede demostrar que:

1. La respuesta final, cuando \(t \rightarrow \infty\), a una entrada sinusoidal de frecuencia angular \(\omega\) es una sinusoidal de la misma frecuencia.

2. La razón de amplitudes (RA) es el módulo de \(G (\mathrm{i} \omega)\):

   \[\mathrm{RA} = |G (\mathrm{i}\omega)|\]

   La respuesta sinusoidal tendrá el siguiente desfase:

   \[\varphi = \arg (G (\mathrm{i}\omega))\]

A continuación se tratan con detalle algunos de los principales sistemas estudiados y se introducen los diagramas de Bode.

8.4.1 Sistemas lineales de primer orden

Para un sistema de primer orden de ganancia k y constante de tiempo \(\tau\):

\[\begin{aligned} \frac{\mathrm{RA}}{k} &= \frac{1}{\sqrt{\tau^2 \omega^2 + 1}} \\ \varphi &= \mathrm{atan} (- \tau \omega) \end{aligned}\]

Una manera conveniente de representar la razón de amplitudes y el desfase son los diagramas de Bode. Estos diagramas consisten en representar la razón de amplitudes frente a la frecuencia angular utilizando escalas logarítmicas y el desfase en una escala lineal frente a la frecuencia angular en una escala logarítmica. Si se desea utilizar solo escalas lineales hay que representar \(\log \mathrm{RA}\) y \(\varphi\) frente al \(\log \omega\). A veces se representa la razón de amplitudes como decibelios:

\[\mathrm{dB}= 20 \log \mathrm{RA}\]

A menudo se representa en los diagramas de Bode \(\frac{\mathrm{RA}}{k}\) y \(\tau \omega\) para obtener diagramas independientes del sistema.

Figura 8.4: Diagrama de Bode para un sistema de primer orden. ABF es la asíntota de baja frecuencia y AAF es la asíntota de alta frecuencia.

Para dibujar el diagrama de Bode de un sistema lineal de primer orden, se debe calcular el logaritmo de la razón de amplitudes:

\[\log \left( \frac{\mathrm{RA}}{k} \right) = - \frac{1}{2} \log (1 + \tau^2 \omega^2)\]

A partir del análisis de la Figura 8.4 se observa que:

1. La razón de amplitudes tiende a 1 cuando la frecuencia tiende a 0. Es decir:

   \[\lim_{\omega \to 0} \frac{\mathrm{RA}}{k} = 1 \Rightarrow \lim_{\omega \to 0} \log \frac{\mathrm{RA}}{k} = 0\]

   Existe para bajas frecuencias una asíntota horizontal que para por el punto (1,1) de la gráfica de razón de amplitudes frente a la frecuencia, es la asíntota de baja frecuencia (ABF).

2. También existe una asíntota de alta frecuencia (AAF), \(\log \frac{\mathrm{RA}}{k} \approx - \log \tau \omega\). Es una recta de pendiente -1 que pasa por el punto (1,1). Este es el punto en el que la diferencia entre el valor de la asíntota y el de la curva es máxima.

3. A partir del estudio de la gráfica de desfase frente a frecuencia se observa que el desfase tiende a 0 cuando la frecuencia tiende a 0.

4. Si la frecuencia tiende a \(\infty\), el desfase tiende a -90°.

5. Si el desfase es de -45°, \(\log \tau \omega = 0\).

8.4.2 Sistema lineal de segundo orden

Para un sistema lineal de 2 orden se puede demostrar que la razón de amplitudes y el desfase se expresan como:

\[\begin{aligned} \mathrm{RA} &= \frac{k}{\sqrt{(1 - \tau^2 \omega^2)^2 + (2 \zeta \tau \omega)^2}}\\ \varphi &= \mathrm{atan} \left( - \frac{2 \zeta \tau \omega}{1 - \tau^2 \omega^2} \right) \end{aligned}\]

Figura 8.5: Diagramas de Bode para diferentes sistemas de 2° orden en función del coeficiente de amortiguamiento.

En este caso, de nuevo aparece una asíntota de bajas frecuencias:

\[\lim_{\omega \to 0} \frac{\mathrm{RA}}{k} = 1\]

y una asíntota para altas frecuencias:

\[\lim_{\omega \to 0} \log \frac{\mathrm{RA}}{k} = - 2 \log \tau \omega\]

A partir del análisis de las gráficas de la figura anterior se observa que el desfase máximo posible es de -180°. Existe un máximo en la razón de amplitudes, si el sistema es subamortiguado, cuando \(\omega \tau = 1\):

\[\begin{aligned} \left( \frac{\mathrm{RA}}{k} \right)_{\max} &= \frac{1}{2 \zeta \sqrt[]{1 - \zeta^2}} \\ \varphi_{\max} &= \sqrt{1 - 2 \zeta^2} \end{aligned}\]

8.4.3 Retraso

En el caso del retraso la razón de amplitudes y el desfase son:

\[\begin{aligned} & \mathrm{RA} = 1 & \\ & \varphi = - t_d \omega & \end{aligned}\]

donde \(t_d\) es el valor del retraso.

Figura 8.6: Diagrama de Bode para el retraso.

8.4.4 Controladores

A continuación se muestra para diferentes controladores las fórmulas utilizadas para la construcción de los diagramas de Bode.

8.4.4.1 Controlador proporcional

Para un controlador proporcional la razón de amplitudes es:

\[\begin{aligned} \mathrm{RA} &= K_c \\ \varphi &= 0 \end{aligned}\]

8.4.4.2 Controlador proporcional+integral

Las ecuaciones necesarias para dibujar el diagrama de Bode de un controlador PI son:

\[\begin{aligned} \mathrm{RA} &= K_c \sqrt[]{1 + \frac{1}{\omega^2 \tau_I^2}}\\ \varphi &= \mathrm{atan} \left( - \frac{1}{\omega \tau_I} \right) \end{aligned}\]

Figura 8.7: Diagrama de Bode para un controlador PI.

En este caso existe, de nuevo, una asíntota de baja frecuencia:

\[\omega \rightarrow 0 \Rightarrow \frac{1}{\omega^2 \tau_I^2} \gg 0 \Rightarrow \log \left( \frac{\mathrm{RA}}{K_c} \right) \rightarrow - \log \omega \tau_I\]

y una asíntota de alta frecuencia:

\[\omega \rightarrow \infty \Rightarrow \frac{1}{\omega^2 \tau_I^2} \rightarrow 0 \Rightarrow \log \left( \frac{\mathrm{RA}}{K_c} \right) \rightarrow 0\]

8.4.4.3 Controlador proporcional+derivativo

En el caso de utilizar un controlador PD:

\[\begin{aligned} \mathrm{RA} &= K_c \sqrt[]{1 + \tau_D^2 w^2}\\ \varphi &= \mathrm{atan} \tau_D \omega > 0 \end{aligned}\]

Figura 8.8: Diagrama de Bode de un controlador PD.

En este caso el desfase aparece adelantado a la entrada. De nuevo se comprueba que la acción derivativa se adelanta al comportamiento futuro de las perturbaciones.

8.4.4.4 Controlador proporcional+integral+derivativo

Para un controlador PID:

\[\begin{aligned} \mathrm{RA} &= K_c \sqrt[]{\left( \tau_D \omega - \frac{1}{\tau_I \omega} \right)^2 + 1} \\ \varphi &= \mathrm{atan} \left( \tau_D \omega - \frac{1}{\tau_I \omega} \right) \end{aligned}\]

Figura 8.9: Diagrama de Bode para un controlador PID con \(\tau_I=10\) y \(\tau_D=0.1\).

8.4.5 Sistemas de varios componentes

Sea un sistema de n procesos en serie cuya dinámica venga descrita por las funciones de transferencia \(G_1, G_2, \ldots, G_n\). Su dinámica global vendrá descrita por la siguiente función de transferencia:

\[G (s) = G_1 (s) G_2 (s) \ldots G_n (s)\]

Se puede demostrar que la razón de amplitudes y el desfase global son:

\[\begin{aligned} & \mathrm{RA} = \mathrm{RA}_1 \mathrm{RA}_2 \ldots \mathrm{RA}_n = \prod_i \mathrm{RA}_i & \\ & \varphi = \varphi_1 + \varphi_2 + \ldots + \varphi_n = \sum_i \varphi_i & \end{aligned}\]

Por tanto,

\[\log \mathrm{RA} = \log \mathrm{RA}_1 + \log \mathrm{RA}_2 + \ldots + \log \mathrm{RA}_n = \sum_i \log \mathrm{RA}_i\]

8.5 Criterio de estabilidad de Bode

Sea el sencillo bucle de retroalimentación de la Figura 8.10. La función de transferencia de lazo abierto de este bucle es:

\[G_{OL} = K\]

Figura 8.10: Bucle de retroalimentación con un controlador proporcional de ganancia unidad.

El criterio de estabilidad de Bode se basa en abrir el bucle e introducir una función sinusoidal para poder estudiar el comportamiento del sistema. En primer lugar se abre el bucle y se introduce una señal sinusoidal de amplitud M y frecuencia angular \(\omega\):

\[y_{sp}(t) = \varepsilon (t) = M \sin \omega t\]

Por tanto, \[y (t) = K M \sin \omega t\] ya que,

\[y (s) = G_{OL} y_{sp} (s)\]

Una vez introducida la señal sinusoidal se cierra el bucle y se devuelve la consigna a su valor inicial \(y_{sp} = 0\). Entonces, \[\varepsilon (t) = - K M \sin \omega t = K M \sin (\omega t - 180^{\circ})\]

De esta manera se ha logrado atrapar la señal sinusoidal dentro del bucle de retroalimentación. Esta señal tiene un desfase de -180 y una amplitud que depende de la ganancia K. Se puede comprobar fácilmente que la razón de amplitudes de la función de la transferencia de lazo abierto (\(G_{OL}\)), entre la entrada \(\varepsilon (t)\) y la salida \(y (t)\), es K:

\[\mathrm{RA} = \frac{\text{Amplitud de la respuesta}}{\text{Amplitude de la entrada}} = \frac{K^2 M}{KM} = K\]

Se puede comprobar de manera muy sencilla que si la razón de amplitudes de lazo abierto es superior a la unidad (\(K > 1\)) el sistema será inestable ya que para cada vuelta del bucle la señal se ve amplificada. Si \(K = 1\), el sistema se encontrará al límite de la estabilidad. Si \(\mathrm{RA} < 1\), la respuesta del sistema global tenderá a cero cuando el tiempo tienda a infinito. Este razonamiento es la base del criterio de estabilidad de Bode:

Importante

Un bucle de control por retroalimentación es inestable si la razón de amplitudes de su función de transferencia de lazo abierto es mayor que la unidad en la frecuencia de cruce \(\omega_{co}\) (crossover frequency), aquella que hace que el desfase sea -180).

Figura 8.11: Aplicación del criterio de estabilidad de Bode. Según el valor de \(K\) la respuesta de lazo cerrado será o no estable.

Para aplicar el criterio de Bode es necesario disponer de los diagramas de Bode de la función de transferencia de lazo abierto del bucle. Estos diagramas se pueden construir:

1. Numéricamente: Conociendo las funciones de transferencia de todos los elementos del bucle.

2. Experimentalmente, en el caso de que todas o alguna de las funciones de transferencia sea desconocida: Para ello se abre el lazo de control y se introducen señales sinusoidales de distintas frecuencias mientras se registran las amplitudes y desfase de las señales sinusoidales de salida. Con esos datos se puede construir el diagrama de Bode.

Tal como se ha visto el criterio de estabilidad de Bode se puede utilizar para sistemas intratables con las técnicas anteriores:

1. Sistemas con función de transferencia compleja

2. Sistemas de los que no se conoce la función de transferencias.

Además proporciona más información para realizar una correcta sintonía del controlador. Aunque también existen sistemas para los que no es aplicable el criterio de estabilidad de Bode.

8.5.1 Márgenes de ganancia y de fase

El criterio de estabilidad de Bode indica cómo establecer un método racional de sintonía de sistemas de control por retroalimentación para evitar situaciones de inestabilidad.

Para aplicar el criterio de estabilidad hay que dibujar los diagramas de Bode de la función de transferencia de lazo abierto. En el diagrama se consideran dos puntos críticos según el criterio de Bode (\(\mathrm{RA} = 1\) y \(\varphi = - 180^{\circ}\)).

Según la Figura 8.12, M es la razón de amplitudes para la frecuencia de cruce. Según el criterio de Bode, M debe ser menor o igual a 1 para que el sistema sea estable.

Figura 8.12: Representación gráfica del margen de ganancia y de fase.

Se puede definir:

\[\text{Margen de ganancia} = \frac{1}{M}\]

Lógicamente debe tomar valores por encima de la unidad para que el sistema sea estable.

El margen de ganancia es una medida importante del sistema ya que:

1. Constituye una medida de la proximidad del sistema de la zona de inestabilidad.

2. Cuanto mayor de la unidad sea el margen de ganancia, más seguro será el sistema controlado.

3. Normalmente se diseñan los controladores para que el margen de ganancia sea mayor de 1.7. Es decir, la razón de amplitudes puede crecer 1.7 veces antes de que el sistema se vuelva inestable. Aunque en el caso de trabajar con procesos muy conocidos puede ser suficiente seleccionar un margen de ganancia entre 1.4 y 1.7. Si los parámetros del sistema son poco conocidos, se recomienda un factor de seguridad entre 1.7 y 3.0.

Además del margen de ganancia se puede establecer otro factor de seguridad:

\[\text{Margen de fase} = 180^{\circ} - |\varphi_{(1)}|\]

donde \(\varphi_{(1)}\) es el desfase para \(\mathrm{RA} = 1\). El margen de fase representa en cuanto hay que aumentar el desfase para inestabilizar el sistema. Se recomienda normalmente valores mayores de 30.

8.6 Criterio de estabilidad de Nyquist

El criterio de estabilidad de Nyquist es una alternativa a los diagramas de Bode para realizar el análisis de estabilidad de procesos. El diagrama de Nyquist contiene la misma información que los de Bode, por lo que su construcción es sencilla a partir de éstos, pero puede tratar sistemas para los que no es aplicable el criterio de estabilidad de Bode.

Figura 8.13: Sistemas para los que el criterio de estabilidad de Bode no es aplicable.

Para dibujar el diagrama de Nyquist se representa \(\mathrm{Im}[G (\mathrm{i}\omega)]\) en ordenadas y \(\mathrm{Re}[G (\mathrm{i}\omega)]\) en abscisas.

Figura 8.14: Curva de Nyquist de un proceso. El punto 1 viene definido por una frecuencia \(\omega\).

Para el punto 1 de la Figura 8.14, definido por su frecuencia \(\omega_1\), se puede observar que:

1. La distancia entre el punto 1 y el (0,0) es:

   \[\mathrm{distancia} = \sqrt{\{\mathrm{Re}[G (\mathrm{i}\omega)]\}^2 + \{\mathrm{Im}[G (\mathrm{i}\omega)]\}^2} = |G(\mathrm{i}\omega)| = \mathrm{Re}\]

2. El ángulo \(\varphi\) de la figura es el desfase para la frecuencia \(\omega_1\):

   \[\varphi = \mathrm{atan}\frac{\mathrm{Im} [G (\mathrm{i}\omega)]}{\mathrm{Re}[G(\mathrm{i}\omega)]} = \arg G (\mathrm{i}\omega) = \mathrm{desfase}\]

Para trazar el diagrama de Nyquist se debe variar la frecuencia entre 0 y \(\infty\) para encontrar la RA y \(\varphi\) y, a continuación, representarlos en el plano complejo. Una vez trazado el diagrama se aplica el criterio de estabilidad de Nyquist (Figura 8.15):

Si la curva de Nyquist de lazo abierto de un sistema de retroalimentación envuelve el punto (-1,0) para frecuencias \(\omega\) desde \(- \infty\) hasta \(\infty\), la respuesta de lazo cerrado será inestable.

Figura 8.15: Curva de Nyquist para dos lazos abiertos. a) Sistema estable, b) Sistema inestable.

El diagrama de Nyquist se puede construir a partir del diagrama de Bode. Ambos diagramas contienen la misma información. El margen de fase y el margen de ganancia también se pueden evaluar en el diagrama de Nyquist.

Figura 8.16: Obtención del margen de ganancia y de fase a partir de la curva de Nyquist.

El punto A de la Figura 8.16 es aquel cuya frecuencia hace que RA sea 1, de manera que \(\varphi_{MF}\) representa el margen de fases. El punto \(B\) tiene un desfase de -180°, de manera que su RA es \(M\). Por tanto, el margen de ganancias es \(\frac{1}{M}\).

8.7 Problemas

Problema 8.1 ★

Estimar la estabilidad de un sistema de control automático cuya función de transferencia de lazo abierto es:

\[GH=\frac{9}{(10 s+1)^3}\]

Solución

Para determinar si el lazo de control es estable se puede utilizar el criterio de Routh. La ecuación característica de este sistema es:

\[\begin{aligned} 1 + G H = 0\\ 1 + \frac{9}{(10 s + 1)^3} = 0\\ 1000 s^3 + 300 s^2 + 30 s + 10 = 0 \end{aligned}\]

La matriz de Routh es:

\[\begin{array}{rr} 1000 & 30\\ 300 & 10\\ -3.33 & \end{array}\]

La primera columna tiene un signo negativo, lo que implica que es sistema es inestable.

Problema 8.2 ★

Considérese un proceso de segundo orden cuya función de transferencia es:

\[G_p = \frac{1}{s^2+2s+1}\]

1. ¿Es estable dicho proceso?

2. Si el proceso se encuentra en un lazo de control, con un controlador PI (\(K_c=100\), \(\tau_I=0.1\)), siendo las funciones de transferencia de los elementos medidor y final de control \(H=G_v=1\), ¿es estable dicho conjunto? (Puede aplicarse el criterio de Routh-Hurvitz)

3. Hacer el análisis de estabilidad de este sistema de lazo de control en función de \(K_c\) y \(\tau_I\).

Solución

1. El diagrama de bloques de este proceso es:

La ecuación característica de este sistema será el numerador de la función de transferencia, ya que el sistema será estable siempre que sus raíces tengan la parte real negativa:

\[s^2 + s + 1 = 0\]

Para comprobar la estabilidad del proceso se puede aplicar el método de Routh-Hurwitz. La matriz de Routh es:

\[\begin{array}{ll} 1 & 1\\ 2 & \\ 1 = \frac{(2) (1)}{2} & \end{array}\]

Todos los elementos de la primera columna son positivos, por tanto, el sistema es estable.

2. Al existir un controlador por retroalimentación, el diagrama de bloques pasa a ser:

En este caso la ecuación característica es:

\[1 + G_c G_p = 0\]

Sustituyendo las funciones de transferencia se obtiene:

\[1 + 100 \left( 1 + \frac{1}{0.1 s} \right) \frac{1}{s^2 + s + 1} = 0\]

Operando se encuentra que:

\[\frac{s^3 + s^2 + 101 s + 1000}{s^3 + s^2 + s} = 0\]

Por tanto:

\[s^3+s^2+101 s+1000=0\]

La matriz de Routh será:

\[\begin{array}{ll} 1 & 101\\ 1 & 1000\\ - 899 & \end{array}\]

El sistema es inestable ya que uno de los elementos de la primera columna tiene signo negativo.

3. La ecuación característica en este caso es:

\[1 + K_c \left( 1 + \frac{1}{\tau_I s} \right) \frac{1}{s^2 + s + 1} = 0\]

Operando se encuentra que:

\[\frac{\tau_I s^3 + \tau_I s^2 + (K_c + 1) \tau_I s + K_c}{\tau_I s^3 + \tau_I s^2 + \tau_I s} = 0\]

Por tanto,

\[\tau_I s^3 + \tau_I s^2 + (K_c + 1) \tau_I s + K_c = 0\]

La matriz de Routh es:

\[\begin{array}{ll} \tau_I & (K_c + 1) \tau_I\\ \tau_I & K_c\\ \frac{\tau_I^2 (K_c + 1) - \tau_I K_c}{\tau_I} & \end{array}\]

Para que el sistema sea estable todos los elementos de la primera columna deben ser positivos, lo que implica que:

\[\tau_I > 0\]

\[\tau_I (K_c + 1) - K_c > 0\]

La constante de tiempo integral y la ganancia del controlador son, por definición, positivas. Resolviendo la inecuación se encuentra que para que el sistema sea positivo se tiene que cumplir la condición:

\[\tau_I > - \frac{K_c}{K_c + 1}\]

o la condición:

\[K_c > \frac{\tau_I}{\tau_I - 1}\]

Problema 8.3

Un sistema tiene una dinámica cuya ecuación característica es:

\[s^4 + 3 s^3 + 5 s^2 + 4 s + 2 = 0\]

Determinar su estabilidad mediante el criterio de Routh.

Problema 8.4

Sea el sistema de control de tercer orden de la figura:

donde:

\[\begin{aligned} G_p &= \frac{1}{(\tau_1s+1)(\tau_2s+1)}\\ G_m &= \frac{1}{\tau_3s+1} \end{aligned}\]

Si \(\tau_1 = 1\), \(\tau_2 = 1 / 2\) y \(\tau_3 = 1 / 3\), determinar los valores de \(K_c\) para los que el sistema de control es estable.

Problema 8.5

Un sistema formado por dos tanques en serie independientes se regula por un control PID. Las constantes de tiempo de los tanques son 20 y 10 min, mientras que las del elemento de medida de nivel es de 30 segundos. El tiempo integral es de 3 min y el derivativo 40 s. Determinar el intervalo de valores de \(K_c\) para los que el lazo de control es estable.

Problema 8.6

  En la actualidad todavía se emplean discos duros en algunos ordenadores para almacenar la información. Un cabezal de lectura se desplaza sobre el disco giratorio a las posiciones requeridas en las operaciones de lectura o grabación de información. Este desplazamiento ha de ser rápido y preciso. En la figura adjunta se presenta el diagrama de bloques del sistema de desplazamiento del cabezal de lectura.

donde:

\[\begin{aligned} G_c &= \frac{K(s+a)}{s+1}\\ G_p &= \frac{1}{s(s+2)(s+3)} \end{aligned}\]

Determinar los intervalos de estabilidad de \(K\) y \(a\). ¿Qué valores podría tomar \(a\) para \(K = 40\)?

Problema 8.7 ★

En la figura se representa el diagrama de bloques de un sistema de control de velocidad de un motor de gasolina:

donde:

\[\begin{aligned} G_c &= \frac{1}{\tau_Is+1}\\ G_e &= \frac{K}{\tau_es+1}\\ G_m &= \frac{1}{\tau_ms+1} \end{aligned}\]

\(\tau_i\) es la constante de tiempo del carburador, igual a 1; \(\tau_e\) es la del motor, igual a 4 segundos; y \(\tau_m\) es la del medidor de velocidad, igual a 0.5 s. Determinar:

1. El valor de la ganancia \(K\) del motor para que, ante una variación \(M\) en la consigna, la velocidad obtenida no difiera respecto a la consigna en más de un 7 % de dicha variación \(M\).

2. La estabilidad del sistema.

3. El margen de la ganancia \(K\) determinada en el primer apartado.

Solución

1. En este apartado se propone un cambio en la consigna consistente en un escalón de altura M:

\[R (s) = \frac{M}{s}\]

La función de transferencia que describe la dinámica de este lazo de control para un cambio en la consigna es:

\[G (s) = \frac{C (s)}{R (s)} = \frac{\frac{1}{s + 1} \frac{K}{4s + 1}}{1 + \frac{1}{s + 1} \frac{K}{4 s + 1} \frac{1}{0.5 s + 1}} = \frac{Ks + 2 K}{4 s^3 + 13 s^2 + 11 s + 2 K + 2}\]

La velocidad estacionaria obtenida será:

\[\lim_{s \to 0} [s G (s) R (s)] = \lim_{s \to 0} \left[ s \frac{Ks + 2 K}{4 s^3 + 13 s^2 + 11 s + 2 K + 2} \frac{M}{s} \right] = \frac{KM}{K + 1}\]

Se desea que la diferencia entre la velocidad obtenida y la deseada no difiera en más de un 7% de \(M\). En este caso se considerará el caso límite de que la diferencia sea de un 7% de \(M\). Por tanto:

\[\frac{KM}{K + 1} = (1 - 0.07) M\]

Es decir,

\[K = 13.28\]

2. Para determinar la estabilidad del sistema se puede recurrir al método de Routh-Hurvitz ya que el sistema es lineal. La ecuación característica de este lazo de control se puede obtener a partir del denominador de la Ecuación 8.1 y es:

\[4 s^3 + 13 s^2 + 11 s + 2 K + 2 = 0\]

También se puede obtener la ecuación característica a partir de:

\[1 + G_{\mathrm{OL}} = 1 + \frac{1}{s + 1} \frac{K}{4 s + 1} \frac{1}{0.5 s + 1} = 0\]

Una vez encontrada la ecuación característica hay que construir la matriz de Routh-Hurvitz:

\[\left(\begin{array}{cc} 4 & 11\\ 13 & 2 K + 2\\ \frac{13 \cdot 11 - 4 (2 K + 2)}{13} = - \frac{8 K - 135}{11} & \end{array}\right)\]

Por tanto, el lazo de control será estable si:

\[- \frac{8 K - 135}{11} \geqslant 0\]

Resolviendo la inecuación se encuentra que el lazo de control será estable si:

\[K \leqslant \frac{135}{8} = 16.875\]

3. La ganancia límite \(K_u\) para la que el lazo de control todavía es estable es:

\[K_u = 16.875\]

Por tanto, el margen de la ganancia \(K\) será:

\[\mathrm{MG} = \frac{K_u}{K} = \frac{16.875}{13.28} = 1.271\]

Lo que significa que la ganancia \(K\) puede aumentar hasta un 27.1% y el lazo de control continuará siendo estable.

Problema 8.8 ★

Sea el sistema de control representado en la figura:

donde \(G_c=K_c\), \(G_1=\frac{1}{(\tau_1s+1)(\tau_2s+1)}\) y \(G_2=\frac{1}{\tau_3s+1}\).

1. Calcular el error permanente de la respuesta del sistema si se produce una carga (\(U\)) en escalón unidad.

2. Si \(\tau_1=1\), \(\tau_2=\frac{1}{2}\) y \(\tau_3=\frac{1}{3}\), ¿para qé valores de ganancia \(Kc\) es estable el sistema?

3. Si se sustituyera el control proporcional por un control PI, siendo \(K_c=5\) y \(\tau_I=0.25\), ¿sería estable el sistema?

Solución

1. La función de transferencia para un cambio en la carga es:

\[\frac{C}{U} = \frac{G_1}{1 + G_c G_1 G_2} = \frac{\tau_3 s + 1}{(\tau_1 s + 1) (\tau_2 s + 1) (\tau_3 s + 1) + K_c}\]

El error permanente para un cambio en la carga en escalón unidad será:

\[\mathrm{offset} = \lim_{s \to 0} \left( s R - s \frac{C}{U} U \right) = \lim_{s \to 0} \left( s 0 - s \frac{C}{U} \frac{1}{s} \right) = - \frac{1}{1 + K_c}\]

2. La ecuación característica de este lazo de control es:

\[1 + G_c G_1 G_2 = 0\]

Obviamente, la parte derecha de la ecuación característica coincide con el denominador de la función de transferencia encontrada en el apartado a). Por tanto,

\[(\tau_1 s + 1) (\tau_2 s + 1) (\tau_3 s + 1) + K_c = 0\]

Sustituyendo se encuentra:

\[0.1667 s^3 + s^2 + 1.833 s + 1 + K_c = 0\]

Para buscar para qué valores de \(K_c\) el sistema es estable se puede recurrir al criterio de Routh-Hurvitz. La matriz de Routh es:

\[\begin{array}{cc} 0.1667 & 1.833\\ 1 & 1 + K_c\\ 1.666 - 0.1667 K_c & \end{array}\]

Para que el sistema sea estable:

\[1.666 - 0.1667 K_c > 0\]

Lo que supone que el sistema será estable para ganancias proporcionales que cumplan la siguiente condición:

\[0 < K_c < 9.994\]

3. Si el controlador proporcional se sustituye por un controlador PI con ganancia \(K_c = 5\) y \(\tau_I = 0.25\), la nueva ecuación característica será:

\[1 + 5 \left( 1 + \frac{1}{0.25 s} \right) \frac{1}{(\tau_1 s + 1) (\tau_2 s + 1)} \frac{1}{\tau_3 s + 1} = 0\]

Sustituyendo y operando se obtiene:

\[4.1667 \cdot 10^{- 2} s^4 + 0.20833 s^3 + 0.375 s^2 + 1.625 s + 5 = 0\]

La matriz de Routh es:

\[\begin{array}{ccc} 4.1667 \cdot 10^{- 2} & 0.375 & 5\\ 0.20833 & 1.625 & \\ 4.9992 \cdot 10^{- 2} & 5 & \\ - 19.211 & & \end{array}\]

En la primera columna de la matriz hay un elemento negativo, lo que implica que el nuevo lazo de control es inestable.

Problema 8.9

Dibujar el lugar de las raíces para un sistema cuya función de transferencia de lazo abierto es:

\[G_c G_f G_p G_m = \frac{K (s + 1)}{s (s + 2)}\]

Problema 8.10 ★

Trazar el lugar de las raíces para el control proporcional de un sistema de tres etapas con constantes de tiempo 1, 0.5 y 0.25 min, ganancia de proceso \(K_p=1\) y medidor \(H=1\). Determinar la estabilidad para los valores de \(K_c\) siguientes: 0.1, 10 y 15. ¿Qué valores tendrán el margen de ganancia y de fase para cada uno de esos tres casos?

Solución

Gráfico del lugar de las raíces

El lazo de control propuesto es:

Por tanto, su ecuación característica es:

\[1 + K_c \frac{1}{s + 1} \frac{1}{0.5 s + 1} \frac{1}{0.25 s + 1} = 0\]

Operando se encuentra:

\[0.125 s^3 + 0.875 s^2 + 1.75 s + 1 + K_c = 0\]

Para dibujar el lugar de las raíces hay que encontrar las raíces de la ecuación anterior para diferentes valores de \(K_c\) y representarlas en el plano complejo.

Empezaremos cargando las librerías necesarias y creando las variables que utilizaremos:

using SymPy, Plots
#plotly()

@syms s, t::real, Kc::real=>"K_c"

(s, t, K_c)

Tal como se indicaba más arriba, la función de lazo abierto es:

Gol_s = Kc*1/(s+1)*1/(.5s+1)*1/(.25s+1)

\(\frac{K_{c}}{\left(0.25 s + 1\right) \left(0.5 s + 1\right) \left(s + 1\right)}\)

Las raíces de la ecuación característica en función de \(K_c\), un polinomio de tercer grado tiene solución analítica:

rl = solve(1+Gol_s, s)

\(\left[\begin{smallmatrix}- 1.5874010519682 \left(-0.5 - 0.866025403784439 i\right) \sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926} - 2.33333333333333 - \frac{0.48996929718134 \left(-0.5 + 0.866025403784439 i\right)}{\sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926}}\\- 1.5874010519682 \left(-0.5 + 0.866025403784439 i\right) \sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926} - 2.33333333333333 - \frac{0.48996929718134 \left(-0.5 - 0.866025403784439 i\right)}{\sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926}}\\- 1.5874010519682 \sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926} - 2.33333333333333 - \frac{0.48996929718134}{\sqrt[3]{K_{c} + \left(\left(K_{c} + 0.0925925925925926\right)^{2} - 0.0294067215363512\right)^{0.5} + 0.0925925925925926}}\end{smallmatrix}\right]\)

Para poder trabajar con la función de una manera más sencilla, vamos a convertirla en una función de Julia:

raiz = lambdify(rl)

#155 (generic function with 1 method)

Comprobamos que funciona calculando las raíces para \(Kc=3\):

raiz(3)

3-element Vector{Number}:
 -0.7432742592131494 + 2.2916217498187774im
 -0.7432742592131494 - 2.2916217498187774im
                    -5.513451481573702

Dibujaremos las raíces de la ecuación característica para valores de \(K_c\) entre 0 y 20:

# Definimos los valores de Kc para los que representaremos el lugar
# de las raíces
K = range(0, 20, step=.1)
lreal = []
limag = []

# Para evitar que se produzca un error en la línea de más abajo:
#    root = raiz(Complex(k))
# https://discourse.julialang.org/t/how-to-extend-cube-root-to-complex-numbers/42509/5
Base.cbrt(z::Complex) = cbrt(abs(z)) * cis(angle(z)/3)

# En este bucle, en primer lugar encontramos las raíces para
# cada valor de Kc
# En el segundo
for k in K
    root = raiz(Complex(k))
    for i in root
        push!(lreal, real(i))
        push!(limag, imag(i))
    end
end

scatter(lreal, limag, legend=false, xlabel="Re", ylabel="Im")

Dibujar el gráfico del lugar de las raíces no es complicado, pero sí es un poco laborioso. Una opción más simple, es utilizar la biblioteca ControlSystems.jl, que dibujar el lugar de las raíces utilizando métodos numéricos:

using ControlSystems

# Definimos la variable s
s = tf("s")

# Representación del lugar de las raíces para Gol para
# valores de Kc entre 0 y 20 
plot(rlocus(1/(s+1)*1/(.5s+1)*1/(.25s+1), K=20))

Pasando el ratón sobre las curvas, se puede leer los valor de la raíces y el valor de la ganancia del controlador:

Valores de las raíces en función de Kc

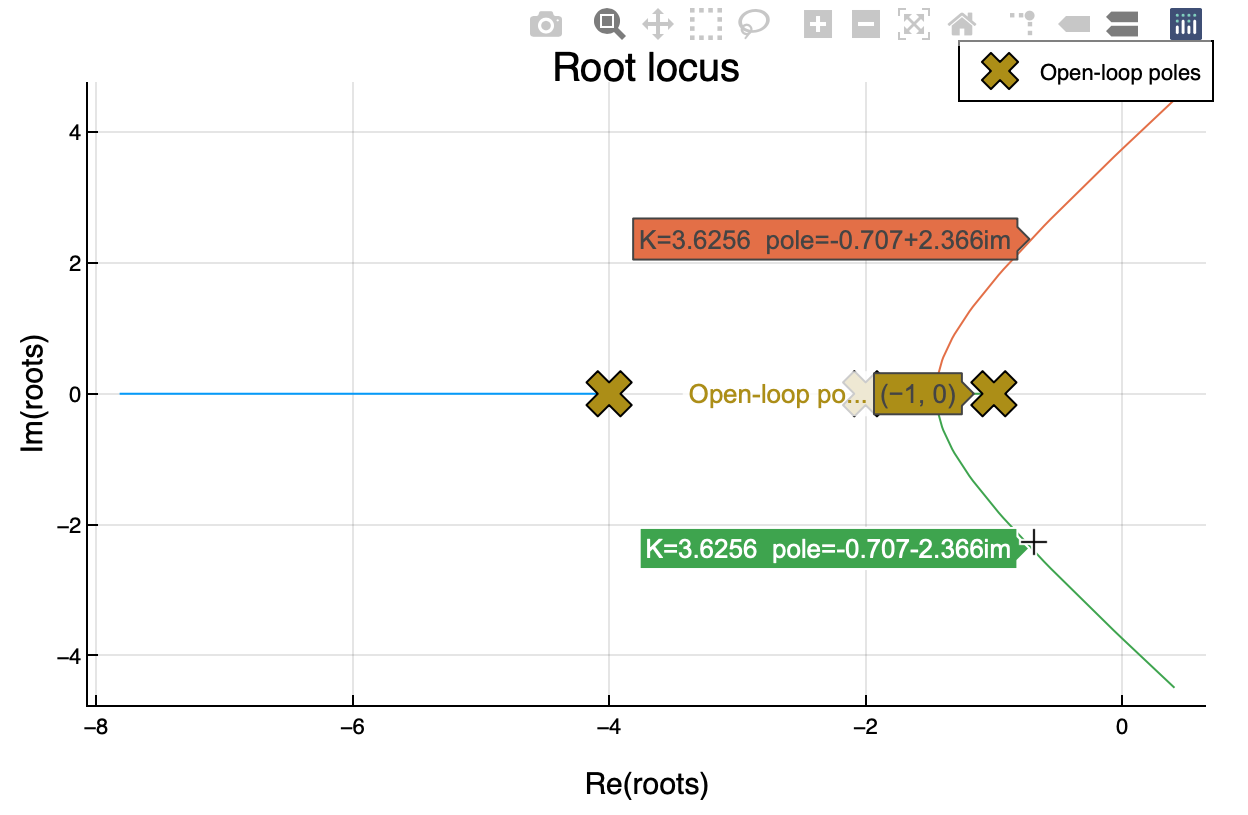
Estudio de estabilidad para los valores de \(K_c\) siguientes: 0.01, 10 y 15

Resolviendo la ecuación característica se puede construir la siguiente tabla:

Kc	raíces
0.01	-1.959 - 0.0im
	-1.028 + 0.0im
	-4.013 + 0.0im
10.0	-0.082 + 3.587im
	-0.082 - 3.587im
	-6.835 + 0.0im
15.0	0.217 + 4.144im
	0.217 - 4.144im
	-7.433 + 0.0im

Se comprueba que dos de las raíces para \(K_c = 10\) tienen la parte real positiva.

A partir del gráfico del lugar de las raíces también se podría haber obtenido la tabla anterior.

Margen de ganancia y de fase

Al conocer la ganancia última del controlador proporcional (\(K_u = 11.3\)), el cálculo del margen de ganancia resulta trivial:

\[\mathrm{MG} = \frac{K_u}{K_c}\]

Por tanto:

\(K_c\)	MG
0.01	1130
10	1.13
15	0.753

También se puede calcular el margen de ganancia mediante análisis de frecuencia. Para ello hay que conocer la razón de amplitudes y el desfase de la función de transferencia de lazo abierto:

\[\begin{aligned} RA_{OL} &= K_c \frac{1}{\sqrt{\omega^2 + 1}} \frac{1}{\sqrt{0.5^2 \omega^2 + 1}} \frac{1}{\sqrt{0.25^2 \omega^2 + 1}}\\ \varphi_{OL} &= \mathrm{atan} (- \omega) + \mathrm{atan}(- 0.5 \omega) + \mathrm{atan} (- 0.25 \omega) \end{aligned}\]

En primer lugar hay que encontrar la frecuencia de cruce (\(\varphi_{OL}(\omega_{co}) = - \pi\)). Tras resolver la ecuación se obtiene que \(\omega_{co} = 3.74 \text{ rad/min}\). Sustituyendo en la razón de amplitudes y fijando el límite de estabilidad (\(RA_{OL}(\omega_{co}) = 1\)), se obtiene:

\[MG = \frac{1}{0.089 K_c}\]

Problema 8.11 ★

El comportamiento dinámico de una compleja organización empresarial se puede considerar que es como un sistema de control por retroalimentación. Un modelo sencillo de un sistema de control de gestión se presenta en la figura adjunta:

con las siguientes funciones de transferencia:

• \(G_c = \frac{k_1}{s}\), correspondiente a la actividad de gestión de la empresa,

• \(G_p = \frac{k_2}{\tau_p s+1}\), correspondiente a las actividades de ingeniería y producción, y,

• \(H = k_4 +k_5s\) que representa la actividad de evaluación de los resultados \(C(s)\) de la empresa.

El resultado de la evaluación, \(B(s)\), se compara con los objetivos propuestos, \(R(s)\), y la diferencia constituye la entrada al bloque de gestión, \(G_c\), que dará lugar a la acción correctora. \(D(s)\) representa las perturbaciones que actúan sobre la empresa.

1. Calcular la constante de tiempo y el coeficiente de amortiguamiento de este sistema de control.

2. Calcular el error permanente si se produce en la carga una perturbación unidad en forma de escalón.

3. La respuesta en tiempo real a la perturbación anterior, ¿es oscilatoria? Si lo es, ¿qué período tiene?

4. Para disminuir el error permanente frente a las variaciones en la consigna, ¿qué parámetro se debería modificar?

5. Estudiar la estabilidad de este sistema de control. ¿Cómo afectaría a la estabilidad la modificación anterior?

Datos:

• \(k_1 k_2\)= 0.1
• \(\tau_p\) = 10 meses
• \(k_4\) = 5
• \(k_5\) = 7.6

Solución

1. La función de transferencia que describe la dinámica de este lazo de control, para una cambio en las perturbaciones (cambio en la carga), es:

\[\frac{C (s)}{D (s)} = \frac{G_p}{1 + G_c G_p H} = \frac{\frac{k_2}{k_1 k_2 k_4} s}{\frac{\tau_p}{k_1 k_2 k_4} s^2 + \frac{1 + k_1 k_2 k_5}{k_1 k_2 k_4} s + 1}\]

Por tanto, la constante de tiempo y el coeficiente de amortiguamiento son:

\[\begin{aligned} \tau &= \sqrt{\frac{\tau_p}{k_1 k_2 k_4}} = 4.4721\\ 2 \tau \zeta &= \frac{1 + k_1 k_2 k_5}{k_1 k_2 k_4} \Rightarrow \zeta = 0.3935 \end{aligned}\]

2. El error permanente para un cambio en la carga de tipo escalón unidad (\(D (s) = 1 / s\)) es:

\[\text{Error permanente} = \lim_{t \to \infty} [R (t) - C (t)] = 0 - \lim_{s \to 0} C (s) = - \lim_{s \to 0} s \frac{C (s)}{D (s)} \frac{1}{s} = 0\]

El error permanente vale 0, lo que significa que la perturbación se anula completamente.

3. La respuesta será oscilatoria, ya que el coeficiente de amortiguamiento es menor que la unidad.

El período de la respuesta sera:

\[T = \frac{2 \pi \tau}{\sqrt{1 - \zeta^2}} = 30.565\]

4. La función de transferencia para cambios en la consigna es:

\[\frac{C (s)}{R (s)} = \frac{G_c G_p}{1 + G_c G_p H} = \frac{\frac{k_1 k_2}{k_1 k_2 k_4}}{\frac{\tau_p}{k_1 k_2 k_4} s^2 + \frac{1 + k_1 k_2 k_5}{k_1 k_2 k_4} s + 1} = \frac{\frac{1}{k_4}}{\tau^2 s^2 + 2 \pi \zeta s + 1}\]

Tal como era de esperar, la constante de tiempo y el coeficiente de amortiguamiento son los mismos que los calculados en el apartado a).

El error permanente para un cambio en la consigna escalón unidad (\(R (s) = 1 / s\)) es:

\[\text{Error permanente} = \lim_{t \to \infty} [R (t) - C (t)] = \lim_{s \to 0} \left[ s \frac{1}{s} - s \frac{C (s)}{R (s)} \frac{1}{s} \right] = 1 - \frac{1}{k_4}\]

El error permanente se reducirá cuando:

\[\lim_{k_4 \to 1} \text{Error permanente} = 0\]

Por tanto, el parámetro a modificar es \(k_4\). Se debe lograr que su valor sea lo más próximo a la unidad posible.

5. Para determinar si el sistema es estable al variar \(k_4\) se puede utilizar el método de Routh. La matriz de Routh es:

\[\begin{array}{ll} \frac{\tau_p}{k_1 k_2 k_4} & 1\\ \frac{1 + k_1 k_2 k_5}{k_1 k_2 k_4} & \\ 1 & \end{array}\]

Se comprueba que el sistema es estable para cualquier valor de \(k_4 > 0\).

Problema 8.12 ★

Un sistema de control utiliza un PI y se representa en el diagrama de bloques de la figura:

Las funciones de transferencia son las siguientes:

\[\begin{aligned} G_v &= k_v\\ G_p &= \frac{1}{(s^2+s+2)(5s+2)}\\ G_{m_1} = \mathrm{e}^{-0.8s}\\ G_{m_2} = k_1 \end{aligned}\]

siendo \(G_c\) la correspondiente a un controlador PI.

Las constantes de las funciones de transferencia son: \(K_c\) = 10, \(\tau_I\) = 1 min, \(k_1\) = 0.25 y \(k_v\) = 0.5.

1. Determinar los márgenes de ganancia y de fase.

2. Mostrar si el sistema es o no estable.

3. ¿Qué influencia tendría la introducción en el controlador de una acción derivativa con \(\tau_D\) = 1 min.

Solución

a) Para resolver este problema se recurrirá a los diagramas de Bode. La función de transferencia de lazo abierto de este sistema es:

\[G_{OL} = G_c G_v G_p G_{m_1} G_{m_2} = K_c \left( 1 + \frac{1}{\tau_I s} \right) k_v \frac{1}{(s^2 + s + 2) (5 s + 2)} \mathrm{e}^{- 0.8 s} k_1\]

Sustituyendo los valores de las constantes:

\[G_{OL} = 4 \left( 1 + \frac{1}{s} \right) \frac{1}{s^2 + s + 2} \frac{1}{5 s + 2} \mathrm{e}^{- 0.8 s} = 4 \left( 1 + \frac{1}{s} \right) \frac{0.5}{0.5 s^2 + 0.5 s + 1} \frac{0.5}{2.5 s + 1} \mathrm{e}^{- 0.8 s}\]

La función de transferencia del proceso \(G_p\) se puede descomponer de manera trivial en el producto de la función de transferencia de un proceso de primer orden y otro de segundo orden. Observar que dichas funciones de transferencia se ha multiplicado y dividido por el término independiente del denominador para obtener las funciones de transferencia de la manera acostumbrada. Si no se hace este paso, fácilmente se pueden obtener constantes de tiempo o coeficientes de amortiguamiento erróneos.

A partir de la función de transferencia de lazo abierto se obtiene la razón de amplitudes y el desfase necesario para obtener el diagrama de Bode:

\[RA_{OL} = 4 \sqrt{1 + \frac{1}{\omega^2}} \frac{0.5}{\sqrt{(1 - 0.5^2 \omega^2)^2 + (0.5 \omega)^2}} \frac{0.5}{\sqrt{2.5^2 \omega^2 + 1}} 1\]

\[\varphi = \mathrm{atan} \left( - \frac{1}{\omega} \right) + \mathrm{atan} \left( - \frac{0.5 \omega}{1 - 0.5^2 \omega^2} \right) + \mathrm{atan} (- 2.5 \omega) - 0.8 \omega\]

Aunque podríamos dibujar el diagrama de Bode con las funciones anteriores, es una tarea un poco tediosa. A continuación se muestra el diagrama de Bode dibujado utilizando SymPy. Para su representación utilizaremos la función bode del paquete ClaseControl:

import ClaseControl

La ayuda de esta función se puede obtener escribiendo:

?ClaseControl.bode

bode(Gol; wmin=1e-1, wmax=1e1, points=100, co=false, ra1=false, RAlabel="RA")

Representación del diagrama de Bode de la función de transferencia Gol.

Parámetros:

• Gol: Función de transferencia dependiente de s

• wmin: Frecuencia angular mínima a representar

• wmax: Frecuencia angular máxima a representar

• points: Número de puntos a representar

• co: Calcula y representa la frecuencia de cruce

• ra1: Calcula y representa la frecuencia que hace que RA = 1

• RAlabel: Etiqueta del gráfico de RA en el diagrama de Bode

Ejemplo:

salida = bode(s->20*(s+1)/s/(s+5)/(s^2+2s+10); wmax=10, co=true, ra1=true)

Para los resultados:

• salida.fig: Diagrama de Bode

• salida.wco y salida.RAco: Frecuencia de cruce y razón de amplitudes para la frecuencia de cruce

• salida.w1 y salida.phi1: Frecuencia para RA = 1 y desfase para RA=1

Las funciones de transferencia del lazo de control nos permiten calcular la función de transferencia de lazo abierto (\(G_{OL}\)):

Gc(s) = 10*(1+1/s)
Gv(s) = 0.5
Gp(s) = 1/((s^2+s+2)*(5s+2))
Gm1(s) = exp(-0.8s)
Gm2(s) = 0.25

Gol(s) = Gc(s)*Gv(s)*Gp(s)*Gm1(s)*Gm2(s)

Gol (generic function with 1 method)

A continuación calculamos el diagrama de Bode para valores de frecuencia angular entre 0.1 y 1. Además, calculamos la frecuencia de cruce y la frecuencia que hace que la razón de amplitudes valga la unidad (\(\omega_1\)):

salida = ClaseControl.bode(Gol; wmax=1, co=true, ra1=true);

El siguiente paso consiste en mostrar el diagrama de Bode:

salida.fig

Obtenemos un valor de frecuencia de cruce:

round(salida.wco, sigdigits=3)

0.781

lo que supone una valor de razón crítica de:

RAcr = salida.RAco
round(RAcr, sigdigits=3)

0.29

Como consecuencia el margen de ganancia, \(MG=\frac{1}{RA_{cr}}\), será:

MG = 1/RAcr
round(MG, sigdigits=3)

3.44

Para obtener el margen de fase, necesitamos el valor del desfase para el que la razón de amplitudes toma el valor de la unidad, \(\varphi_1\). Es decir:

MF = 180 + salida.phi1*180/pi

50.15353175315704

2. El sistema es estable, ya que la razón de amplitudes crítica es superior a la unidad.

3. Al añadir al controlador una acción derivativa (\(\tau_D = 1 \min\)) cambia la función de transferencia de lazo abierto del bucle de control:

\[G_{OL} = 4 \left( 1 + \frac{1}{s} + 1 s \right) \frac{0.5}{0.5 s^2 + 0.5 s + 1} \frac{0.5}{2.5 s + 1} \mathrm{e}^{- 0.8 s}\]

Gc(s) = 10*(1+1/s + 1*s)
Gv(s) = 0.5
Gp(s) = 1/((s^2+s+2)*(5s+2))
Gm1(s) = exp(-0.8s)
Gm2(s) = 0.25

Gol(s) = Gc(s)*Gv(s)*Gp(s)*Gm1(s)*Gm2(s)

Gol (generic function with 1 method)

El nuevo diagrama de Bode es:

salida_c = ClaseControl.bode(Gol; wmax=10, co=true);
salida_c.fig

Al añadir la acción derivativa, la frecuencia de cruce y la razón crítica pasan a tomar los siguientes valores:

round(salida_c.wco, sigdigits=3)

1.29

RAcr = salida_c.RAco
round(RAcr, sigdigits=3)

0.156

Lo que significa que el margen de ganancia es:

MG = 1/RAcr
round(MG, sigdigits=3)

6.4

Todo esto supone que el lazo de control con el controlador PID está más alejado de la zona de inestabilidad, lo que supone que se tratará de un sistema más robusto. Será mucho más difícil que el sistema entre en la zona inestable debido a un error en la estimación de alguna de las ganancias o del retraso, por ejemplo.

Problema 8.13

Dibujar el diagrama de Nyquist de la función de transferencia de lazo abierto siguiente:

\[GH=\frac{1}{s+1}\]

Problema 8.14

Determinar utilizando el criterio de Nyquist la estabilidad de lazo cerrado que tiene la siguiente función de transferencia de lazo abierto:

\[GH = \frac{\frac{k_c}{8}}{(s+1)^3}\]

Problema 8.15

Dibujar los diagramas de Bode y de Nyquist para la siguiente función de transferencia. Discutir la estabilidad.

\[G(s)=\frac{1}{(s+1)(2s+1)}\]

Problema 8.16 ★

Considerar la función de lazo abierto siguiente:

\[G=\frac{K_c}{0.5s+1} \mathrm{e}^{-t_d s}\]

Estudiar mediante los diagramas de Bode la influencia del retraso o del tiempo muerto \(t_d\) y de la ganancia \(K_c\) en la estabilidad del correspondiente lazo cerrado. Como ejemplo, considerar los casos en los que el retraso vale 0.01, 0.1 y 1 min.

Solución

En primer lugar cargamos las bibliotecas necesarias y definimos las variables que utilizaremos para resolver el problema, \(K_c\) y \(t_d\):

import ClaseControl

@syms td::positive=>"t_d" Kc::positive=>"K_c"

(t_d, K_c)

El siguiente paso es definir la función de lazo abierto, \(G_{OL}/K_c\):

Gol_Kc(s, td) = 1/(0.5*s+1)*exp(-td*s)

Gol_Kc (generic function with 1 method)

Para comprobar el efecto del retraso sobre la ganancia del controlador, calcularemos la ganancia última, \(K_u\), para los tres valores de retraso propuestos en el enunciado del problema.

• \(t_d = 0.01\)

  Dibujamos el diagrama de Bode y encontramos \(M = \frac{RA}{K_c(\omega_{co})}\), lo que significa que la ganancia última es:

  \[K_u = \frac{1}{M}\]

sol1 = ClaseControl.bode(s->Gol_Kc(s, 0.01); wmax=300, co=true, RAlabel="RA/Kc")
sol1.fig

# Ganancia última
round(1/sol1.RAco, sigdigits=3)

79.2

• \(t_d = 0.1\)

sol2 = ClaseControl.bode(s->Gol_Kc(s, 0.1); wmin=1, wmax=100, co=true)
sol2.fig

round(1/sol2.RAco, sigdigits=3)

8.5

• \(t_d = 1\)

sol3 = ClaseControl.bode(s->Gol_Kc(s, 1); wmin=1, wmax=10, co=true, RAlabel="RA/Kc")
sol3.fig

round(1/sol3.RAco, sigdigits=3)

1.52

Se comprueba el efecto negativo del retraso sobre la estabilidad del lazo de control. Cuanto mayor es el retraso, menor debe ser la ganancia proporcional última:

td	Kc
0.01	79.2
0.1	8.50
1	1.52

Problema 8.17

Sea un proceso con la siguiente función de transferencia:

\[G_p = \frac{10}{s + 1} \mathrm{e}^{- t_d s}\]

Este proceso se controla mediante un controlador proporcional. Asumiendo que \(G_m = G_f = 1\), determinar la relación entre \(K_c\) y \(t_d\) que hace al lazo cerrado estable en los siguientes casos:

1. Aproximar el retraso con una aproximación de Padé de primer orden:

   \[\mathrm{e}^{- t_d s} \approx \frac{1 - \frac{t_d}{2} s}{1 + \frac{t_d}{2}s}\]

2. Utilizar una aproximación de Padé para el retraso de segundo orden:

   \[\mathrm{e}^{- t_d s} \approx \frac{t_d^2 s^2 - 6 t_d s + 12}{t_d^2 s^2 + 6 t_d s - 12}\]

Problema 8.18 ★

A continuación se muestran la razón de amplitud y desfase en función de la frecuencia de tres sistemas desconocidos:

• Sistema 1:

\(\omega\) (ciclos/min)	RA	\(\phi\) (°)
0.01	10	-0.63
0.05	9.99	-3.15
0.10	9.99	-6.30
1.0	9.95	-63.01
3.0	9.58	-188.60
5.0	8.94	-313.04
7.0	8.19	-436.06
9.0	7.43	-557.65
10.0	7.04	-617.96
12.0	6.40	-737.74
15.0	5.55	-915.75
20.0	4.47	-1209.35
30.0	3.16	etc.
40.0	2.43
50.0	1.96

• Sistema 2:

\(\omega\) (ciclos/min)	RA	\(\phi\) (°)
0.01	5.00	-0.23
0.05	5.05	-1.13
0.10	5.20	-2.39
0.20	5.93	-5.44
0.30	7.68	-11.62
0.40	12.69	-23.96
0.50	25.00	-90.00
0.60	9.98	-151.39
0.70	5.00	-163.74
0.80	3.25	-168.10
0.90	2.20	-170.87
1.10	1.29	-173.46
1.50	0.62	-175.71
2.00	0.33	-176.95
5.00	0.05	-178.84

• Sistema 3:

\(\omega\) (ciclos/min)	RA	\(\phi\) (°)
0.01	17	-1.49
0.02	16.99	-2.98
0.10	16.67	-14.75
0.30	14.42	-41.21
0.50	11.66	-61.90
0.70	9.33	-77.76
1.00	6.80	-95.73
1.50	4.30	-117.03
2.00	2.92	-132.42
2.50	2.07	-144.53
3.00	1.55	-154.04
4.00	0.94	-169.23
8.00	0.26	-208.22
10.00	0.17	-223.12
20.00	0.04	-287.45

1. Determinar el orden de los sistemas y buscar la existencia de tiempos muertos.

2. Calcular los valores de los parámetros de los sistemas, incluido el retraso, si existe.

Solución

Sistema 1

El primer paso será realizar una representación gráfica de los datos:

w_1 = [0.01, 0.05, 0.10, 1.0, 3.0, 5.0, 7.0, 9.0, 10.0, 12.0, 15.0, 20.0]

RA_1 = [10, 9.99, 9.99, 9.95, 9.58, 8.94, 8.19, 7.43, 7.04, 6.40, 5.55, 4.47]

phi_1 = [-0.63, -3.15, -6.30, -63.01, -188.60, -313.04, -436.06, -557.65, -617.96, -737.74, -915.75, -1209.35];

using Plots

scatter(w_1, RA_1, xscale=:log10, yscale=:log10,
    xlabel="ω₁", ylabel="RA₁", legend=false)

scatter(w_1, phi_1, xscale=:log10,
    xlabel="ω₁", ylabel="φ₁", legend=false)

Observando la tabla de razón de amplitudes y desfase de la tabla para el Sistema 1 y su representación gráfica se obtienen las dos conclusiones siguientes:

1. Se trata de un sistema de primer orden o de segundo orden sobreamortiguado, ya que la razón de amplitudes decrece a medida que aumenta la frecuencia angular.

2. El desfase disminuye de manera no asintótica al aumentar la frecuencia angular.

Los parámetros del sistema se pueden obtener de diversas maneras:

Resolución gráfica

Se puede suponer que se trata de un sistema de primer orden con retraso, lo que implica:

\[\begin{aligned} \text{Razón de Amplitudes: } & RA = \frac{K}{\sqrt{1 + \tau^2 \omega^2}} \\ \text{Desfase: } & \varphi = \frac{180}{\pi} [\mathrm{atan} (-\tau \omega) - t_d \omega] \end{aligned}\]

Se puede determinar la ganancia del proceso utilizando la asíntota de baja frecuencia, es decir, sabiendo que:

\[\mathrm{ABF} = \lim_{\omega \to 0} = \frac{K}{\sqrt{1 + \tau^2 \omega^2}} = K\]

La ganancia del sistema coincidirá con el valor de la razón de amplitudes a baja frecuencia. Por tanto:

\[K = 10\]

Utilizando la asíntota de alta frecuencia se puede encontrar la constante de tiempo del sistema:

\[\mathrm{AAF} = \log RA \approx \log K - \log \tau \omega = \log K - \log \tau - \log \omega\]

La asíntota de alta frecuencia es una recta de pendiente -1 y cuya ordenada en el origen es \(\log K - \log \tau\). Gráficamente se puede encontrar la AAF al representar \(\log RA\) frente a \(\log \omega\). Se obtiene la siguiente recta:

\[\log RA = - \log \omega - 1.991\]

Por tanto, sabiendo que \(K = 10\), se obtiene la siguiente constante de tiempo del sistema:

\[\tau = 0.10\]

Para encontrar el valor del retraso será necesario recurrir a los datos del desfase. Despejando de la ec. (2) se obtiene:

\[\varphi \frac{\pi}{180} + \mathrm{atan} (- \omega \tau) = - t_d \omega\]

Tomando los 8 últimos puntos para los que se dispone de información sobre el desfase se obtiene el siguiente retraso (pendiente de la recta que ajusta los puntos según la ecuación anterior):

\[t_d = -1.0\]

Podemos comprobar la suposición de que el sistema es de primer orden con retraso representando la razón de amplitudes y el desfase del modelo junto con los datos experimentales. Para ello utilizaremos el paquete siguiente, que utilizaremos con el resto de sistemas del problema:

using ClaseControl
G1(s) = 10/(0.1s+1)*exp(-1.0s)

ClaseControl.bode(G1)

ClaseControl.Bode(PlutoPlotly.PlutoPlot(data: [
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis"
]

layout: "layout with fields margin, showlegend, template, xaxis1, xaxis2, yaxis1, and yaxis2"

, Dict{String, Vector{HypertextLiteral.JavaScript}}(), Dict{String, Vector{HypertextLiteral.JavaScript}}(), String[], PlutoPlotly.ScriptContents(HypertextLiteral.JavaScript[HypertextLiteral.JavaScript("// Flag to check if this cell was  manually ran or reactively ran\nconst firstRun = this ? false : true\nconst CONTAINER = this ?? html`<div class='plutoplotly-container'>`\nconst PLOT = CONTAINER.querySelector('.js-plotly-plot') ?? CONTAINER.appendChild(html`<div>`)\nconst parent = CONTAINER.parentElement\n// We use a controller to remove event listeners upon invalidation\nconst controller = new AbortController()\n// We have to add this to keep supporting @bind with the old API using PLOT\nPLOT.addEventListener('input', (e) => {\n\tCONTAINER.value = PLOT.value\n\tif (e.bubbles) {\n\t\treturn\n\t}\n\tCONTAINER.dispatchEvent(new CustomEvent('input'))\n}, { signal: controller.signal })\n"), HypertextLiteral.JavaScript("\t// This create the style subdiv on first run\n\tfirstRun && CONTAINER.appendChild(html`\n\t<style>\n\t.plutoplotly-container {\n\t\twidth: 100%;\n\t\theight: 100%;\n\t\tmin-height: 0;\n\t\tmin-width: 0;\n\t}\n\t.plutoplotly-container .js-plotly-plot .plotly div {\n\t\tmargin: 0 auto; // This centers the plot\n\t}\n\t.plutoplotly-container.popped-out {\n\t\toverflow: auto;\n\t\tz-index: 1000;\n\t\tposition: fixed;\n\t\tresize: both;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\tborder-top-left-radius: 0px;\n\t\tborder-top-right-radius: 0px;\n\t}\n\t.plutoplotly-clipboard-header {\n\t\tdisplay: flex;\n\t\tflex-flow: row wrap;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-top-left-radius: 12px;\n\t\tborder-top-right-radius: 12px;\n\t\tposition: fixed;\n\t\tz-index: 1001;\n\t\tcursor: move;\n\t\ttransform: translate(0px, -100%);\n\t\tpadding: 5px;\n\t}\n\t.plutoplotly-clipboard-header span {\n\t\tdisplay: inline-block;\n\t\tflex: 1\n\t}\n\t.plutoplotly-clipboard-header.hidden {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span {\n\t\tposition: relative;\n\t}\n\t.clipboard-value {\n\t\tpadding-right: 5px;\n\t\tpadding-left: 2px;\n\t\tcursor: text;\n\t}\n\t.clipboard-span.format {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span.filename {\n\t\tflex: 0 0 100%;\n\t\ttext-align: center;\n\t\tborder-top: 3px solid var(--kbd-border-color);\n\t\tmargin-top: 5px;\n\t\tdisplay: none;\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.filename {\n\t\tdisplay: inline-block;\n\t}\n\t.clipboard-value.filename {\n\t\tmargin-left: 3px;\n\t\ttext-align: left;\n\t\tmin-width: min(60%, min-content);\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.format {\n\t\tdisplay: inline-flex;\n\t}\n\t.clipboard-span.format .label {\n\t\tflex: 0 0 0;\n\t}\n\t.clipboard-value.format {\n\t\tposition: relative;\n\t\tflex: 1 0 auto;\n\t\tmin-width: 30px;\n\t\tmargin-right: 10px;\n\t}\n\tdiv.format-options {\n\t\tdisplay: inline-flex;\n\t\tflex-flow: column;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder-radius: 12px;\n\t\tpadding-left: 3px;\n\t\tz-index: 2000;\n\t}\n\tdiv.format-options:hover {\n\t\tcursor: pointer;\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tpadding: 3px;\n\t\ttransform: translate(-3px, -6px);\n\t}\n\tdiv.format-options .format-option {\n\t\tdisplay: none;\n\t}\n\tdiv.format-options:hover .format-option {\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:not(.selected) {\n\t\tmargin-top: 3px;\n\t}\n\tdiv.format-options .format-option.selected {\n\t\torder: -1;\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:hover {\n\t\tbackground-color: var(--kbd-border-color);\n\t}\n\tspan.config-value {\n\t\tfont-weight: normal;\n\t\tcolor: var(--pluto-output-color);\n\t\tdisplay: none;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\ttransform: translate(0px, calc(-100% - 10px));\n\t\tpadding: 5px;\n\t}\n\t.label {\n\t\tuser-select: none;\n\t}\n\t.label:hover span.config-value {\n\t\tdisplay: inline-block;\n\t\tmin-width: 150px;\n\t}\n\t.clipboard-span.matching-config .label {\n\t\tcolor: var(--cm-macro-color);\n\t\tfont-weight: bold;\n\t}\n\t.clipboard-span.different-config .label {\n\t\tcolor: var(--cm-tag-color);\n\t\tfont-weight: bold;\n\t}\n</style>\n`)\n"), HypertextLiteral.JavaScript("let original_height = plot_obj.layout.height\nlet original_width = plot_obj.layout.width\n// For the height we have to also put a fixed value in case the plot is put on a non-fixed-size container (like the default wrapper)\n// We define a variable to check whether we still have to remove the fixed height\nlet remove_container_size = firstRun\nlet container_height = original_height ?? PLOT.container_height ?? 400\nCONTAINER.style.height = container_height + 'px'\n"), HypertextLiteral.JavaScript("// We create a Promise version of setTimeout\nfunction delay(ms) {\n  return new Promise((resolve) => setTimeout(resolve, ms));\n}\n\n// We import interact for dragging/resizing\nconst { default: interact } = await import('https://esm.sh/interactjs@1.10.19')\n\n\nfunction getImageOptions() {\n  const o = plot_obj.config.toImageButtonOptions ?? {};\n  return {\n    format: o.format ?? \"png\",\n    width: o.width ?? original_width,\n    height: o.height ?? original_height,\n    scale: o.scale ?? 1,\n    filename: o.filename ?? \"newplot\",\n  };\n}\n\nconst CLIPBOARD_HEADER =\n  CONTAINER.querySelector(\".plutoplotly-clipboard-header\") ??\n  CONTAINER.insertAdjacentElement(\n    \"afterbegin\",\n    html`<div class=\"plutoplotly-clipboard-header hidden\">\n      <span class=\"clipboard-span format\"\n        ><span class=\"label\">Format:</span\n        ><span class=\"clipboard-value format\"></span\n      ></span>\n      <span class=\"clipboard-span width\"\n        ><span class=\"label\">Width:</span\n        ><span class=\"clipboard-value width\"></span>px</span\n      >\n      <span class=\"clipboard-span height\"\n        ><span class=\"label\">Height:</span\n        ><span class=\"clipboard-value height\"></span>px</span\n      >\n      <span class=\"clipboard-span scale\"\n        ><span class=\"label\">Scale:</span\n        ><span class=\"clipboard-value scale\"></span\n      ></span>\n      <button class=\"clipboard-span set\">Set</button>\n      <button class=\"clipboard-span unset\">Unset</button>\n      <span class=\"clipboard-span filename\"\n        ><span class=\"label\">Filename:</span\n        ><span class=\"clipboard-value filename\"></span\n      ></span>\n    </div>`\n  );\n\nfunction checkConfigSync(container) {\n  const valid_classes = [\n    \"missing-config\",\n    \"matching-config\",\n    \"different-config\",\n  ];\n  function setClass(cl) {\n    for (const name of valid_classes) {\n      container.classList.toggle(name, name == cl);\n    }\n  }\n  // We use the custom getters we'll set up in the container\n  const { ui_value, config_value, config_span, key } = container;\n  if (config_value === undefined) {\n    setClass(\"missing-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> is not present in the config.`;\n  } else if (ui_value == config_value) {\n    setClass(\"matching-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has the same value in the config and in the header.`;\n  } else {\n    setClass(\"different-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has a different value (<em>\${config_value}</em>) in the config.`;\n  }\n  // Add info about setting and unsetting\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click on the label <em><b>once</b></em> to set the current UI value in the config.`\n  );\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click <em><b>twice</b></em> to remove this key from the config.`\n  );\n}\n\nconst valid_formats = [\"png\", \"svg\", \"webp\", \"jpeg\", \"full-json\"];\nfunction initializeUIValueSpan(span, key, value) {\n  const container = span.closest(\".clipboard-span\");\n  span.contentEditable = key === \"format\" ? \"false\" : \"true\";\n  let parse = (x) => x;\n  let update = (x) => (span.textContent = x);\n  if (key === \"width\" || key === \"height\") {\n    parse = (x) => Math.round(parseFloat(x));\n  } else if (key === \"scale\") {\n    parse = parseFloat;\n  } else if (key === \"format\") {\n    // We remove contentEditable\n    span.contentEditable = \"false\";\n    // Here we first add the subspans for each option\n    const opts_div = span.appendChild(html`<div class=\"format-options\"></div>`);\n    for (const fmt of valid_formats) {\n      const opt = opts_div.appendChild(\n        html`<span class=\"format-option \${fmt}\">\${fmt}</span>`\n      );\n      opt.onclick = (e) => {\n        span.value = opt.textContent;\n      };\n    }\n    parse = (x) => {\n      return valid_formats.includes(x) ? x : localValue;\n    };\n    update = (x) => {\n      for (const opt of opts_div.children) {\n        opt.classList.toggle(\"selected\", opt.textContent === x);\n      }\n    };\n  } else {\n    // We only have filename here\n  }\n  let localValue;\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return localValue;\n    },\n    set: (val) => {\n      if (val !== \"\") {\n        localValue = parse(val);\n      }\n      update(localValue);\n      checkConfigSync(container);\n    },\n  });\n  // We also assign a listener so that the editable is blurred when enter is pressed\n  span.onkeydown = (e) => {\n    if (e.keyCode === 13) {\n      e.preventDefault();\n      span.blur();\n    }\n  };\n  span.value = value;\n}\n\nfunction initializeConfigValueSpan(span, key) {\n  // Here we mostly want to define the setter and getter\n  const container = span.closest(\".clipboard-span\");\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return plot_obj.config.toImageButtonOptions[key];\n    },\n    set: (val) => {\n      // if undefined is passed, we remove the entry from the options\n      if (val === undefined) {\n        delete plot_obj.config.toImageButtonOptions[key];\n      } else {\n        plot_obj.config.toImageButtonOptions[key] = val;\n      }\n      checkConfigSync(container);\n    },\n  });\n}\n\nconst config_spans = {};\nfor (const [key, value] of Object.entries(getImageOptions())) {\n  const container = CLIPBOARD_HEADER.querySelector(`.clipboard-span.\${key}`);\n  const label = container.querySelector(\".label\");\n  // We give the label a function that on single click will set the current value and with double click will unset it\n  label.onclick = DualClick(\n    () => {\n      container.config_value = container.ui_value;\n    },\n    (e) => {\n      console.log(\"e\", e);\n      e.preventDefault();\n      container.config_value = undefined;\n    }\n  );\n  const ui_value_span = container.querySelector(\".clipboard-value\");\n  const config_value_span =\n    container.querySelector(\".config-value\") ??\n    label.insertAdjacentElement(\n      \"afterbegin\",\n      html`<span class=\"config-value\"></span>`\n    );\n  // Assing the two spans as properties of the containing span\n  container.ui_span = ui_value_span;\n  container.config_span = config_value_span;\n  container.key = key;\n  config_spans[key] = container;\n  if (firstRun) {\n    plot_obj.config.toImageButtonOptions =\n      plot_obj.config.toImageButtonOptions ?? {};\n    // We do the initialization of the value span\n    initializeUIValueSpan(ui_value_span, key, value);\n    // Then we initialize the config value\n    initializeConfigValueSpan(config_value_span, key);\n    // We put some convenience getters/setters\n    // ui_value forward\n    Object.defineProperty(container, \"ui_value\", {\n      get: () => ui_value_span.value,\n      set: (val) => {\n        ui_value_span.value = val;\n      },\n    });\n    // config_value forward\n    Object.defineProperty(container, \"config_value\", {\n      get: () => config_value_span.value,\n      set: (val) => {\n        config_value_span.value = val;\n      },\n    });\n  }\n}\n\n// These objects will contain the default value\n\n// This code updates the image options in the PLOT config with the provided ones\nfunction setImageOptions(o) {\n  for (const [key, container] of Object.entries(config_spans)) {\n    container.config_value = o[key];\n  }\n}\nfunction unsetImageOptions() {\n  setImageOptions({});\n}\n\nconst set_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.set\");\nconst unset_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.unset\");\nif (firstRun) {\n  set_button.onclick = (e) => {\n    for (const container of Object.values(config_spans)) {\n      container.config_value = container.ui_value;\n    }\n  };\n  unset_button.onclick = unsetImageOptions;\n}\n\n// We add a function to check if the clipboard is popped out\nCONTAINER.isPoppedOut = () => {\n  return CONTAINER.classList.contains(\"popped-out\");\n};\n\nCLIPBOARD_HEADER.onmousedown = function (event) {\n  if (event.target.matches(\"span.clipboard-value\")) {\n    console.log(\"We don't move!\");\n    return;\n  }\n  const start = {\n    left: parseFloat(CONTAINER.style.left),\n    top: parseFloat(CONTAINER.style.top),\n    X: event.pageX,\n    Y: event.pageY,\n  };\n  function moveAt(event, start) {\n    const top = event.pageY - start.Y + start.top + \"px\";\n    const left = event.pageX - start.X + start.left + \"px\";\n    CLIPBOARD_HEADER.style.left = left;\n    CONTAINER.style.left = left;\n    CONTAINER.style.top = top;\n  }\n\n  // move our absolutely positioned ball under the pointer\n  moveAt(event, start);\n  function onMouseMove(event) {\n    moveAt(event, start);\n  }\n\n  // We use this to remove the mousemove when clicking outside of the container\n  const controller = new AbortController();\n\n  // move the container on mousemove\n  document.addEventListener(\"mousemove\", onMouseMove, {\n    signal: controller.signal,\n  });\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        cleanUp();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n\n  function cleanUp() {\n    console.log(\"cleaning up the plot move listener\");\n    controller.abort();\n    CLIPBOARD_HEADER.onmouseup = null;\n  }\n\n  // (3) drop the ball, remove unneeded handlers\n  CLIPBOARD_HEADER.onmouseup = cleanUp;\n};\n\nfunction sendToClipboard(blob) {\n  if (!navigator.clipboard) {\n    alert(\n      \"The Clipboard API does not seem to be available, make sure the Pluto notebook is being used from either localhost or an https source.\"\n    );\n  }\n  navigator.clipboard\n    .write([\n      new ClipboardItem({\n        // The key is determined dynamically based on the blob's type.\n        [blob.type]: blob,\n      }),\n    ])\n    .then(\n      function () {\n        console.log(\"Async: Copying to clipboard was successful!\");\n      },\n      function (err) {\n        console.error(\"Async: Could not copy text: \", err);\n      }\n    );\n}\n\nfunction copyImageToClipboard() {\n  // We extract the image options from the provided parameters (if they exist)\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key. We also ignore format because the clipboard only supports png.\n    if (val === undefined || key === \"format\") {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.toImage(PLOT, config).then(function (dataUrl) {\n    fetch(dataUrl)\n      .then((res) => res.blob())\n      .then((blob) => {\n        const paste_receiver = document.querySelector('paste-receiver.plutoplotly')\n        if (paste_receiver) {\n          paste_receiver.attachImage(dataUrl, CONTAINER)\n        }\n        sendToClipboard(blob)\n      });\n  });\n}\n\nfunction saveImageToFile() {\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key.\n    if (val === undefined) {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.downloadImage(PLOT, config);\n}\n\nlet container_rect = { width: 0, height: 0, top: 0, left: 0 };\nfunction unpop_container(cl) {\n  CONTAINER.classList.toggle(\"popped-out\", false);\n  CONTAINER.classList.toggle(cl, false);\n  // We fix the height back to the value it had before popout, also setting the flag to signal that upon first resize we remove the fixed inline-style\n  CONTAINER.style.height = container_rect.height + \"px\";\n  remove_container_size = true;\n  // We set the other fixed inline-styles to null\n  CONTAINER.style.width = \"\";\n  CONTAINER.style.top = \"\";\n  CONTAINER.style.left = \"\";\n  // We also remove the CLIPBOARD_HEADER\n  CLIPBOARD_HEADER.style.width = \"\";\n  CLIPBOARD_HEADER.style.left = \"\";\n  // Finally we remove the hidden class to the header\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", true);\n  return;\n}\nfunction popout_container(opts) {\n  const cl = opts?.cl;\n  const target_container_size = opts?.target_container_size ?? {};\n  const target_plot_size = opts?.target_plot_size ?? {};\n  if (CONTAINER.isPoppedOut()) {\n    return unpop_container(cl);\n  }\n  CONTAINER.classList.toggle(cl, cl === undefined ? false : true);\n  // We extract the current size of the container, save them and fix them\n  const { width, height, top, left } = CONTAINER.getBoundingClientRect();\n  container_rect = { width, height, top, left };\n  // We save the current plot size before we pop as it will fill the screen\n  const current_plot_size = {\n    width: PLOT._fullLayout.width,\n    height: PLOT._fullLayout.height,\n  };\n  // We have to save the pad data before popping so we can resize precisely\n  const pad = {};\n  pad.unpopped = getSizeData().container_pad;\n  CONTAINER.classList.toggle(\"popped-out\", true);\n  pad.popped = getSizeData().container_pad;\n  // We do top and left based on the current rect\n  for (const key of [\"top\", \"left\"]) {\n    const start_val = target_container_size[key] ?? container_rect[key];\n    let offset = 0;\n    for (const kind of [\"padding\", \"border\"]) {\n      offset += pad.popped[kind][key] - pad.unpopped[kind][key];\n    }\n    CONTAINER.style[key] = start_val - offset + \"px\";\n    if (key === \"left\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  // We compute the width and height depending on eventual config data\n  const csz = computeContainerSize({\n    width:\n      target_plot_size.width ??\n      config_spans.width.config_value ??\n      current_plot_size.width,\n    height:\n      target_plot_size.height ??\n      config_spans.height.config_value ??\n      current_plot_size.height,\n  });\n  for (const key of [\"width\", \"height\"]) {\n    const val = target_container_size[key] ?? csz[key];\n    CONTAINER.style[key] = val + \"px\";\n    if (key === \"width\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", false);\n  const controller = new AbortController();\n\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        unpop_container();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n}\n\nCONTAINER.popOut = popout_container;\n\nfunction DualClick(single_func, dbl_func) {\n  let nclicks = 0;\n  return function (...args) {\n    nclicks += 1;\n    if (nclicks > 1) {\n      dbl_func(...args);\n      nclicks = 0;\n    } else {\n      delay(300).then(() => {\n        if (nclicks == 1) {\n          single_func(...args);\n        }\n        nclicks = 0;\n      });\n    }\n  };\n}\n\n// We remove the default download image button\nplot_obj.config.modeBarButtonsToRemove = _.union(\n  plot_obj.config.modeBarButtonsToRemove,\n  [\"toImage\"]\n);\n// We add the custom button to the modebar\nplot_obj.config.modeBarButtonsToAdd = _.union(\n  plot_obj.config.modeBarButtonsToAdd,\n  [\n    {\n      name: \"Copy PNG to Clipboard\",\n      icon: {\n        height: 520,\n        width: 520,\n        path: \"M280 64h40c35.3 0 64 28.7 64 64V448c0 35.3-28.7 64-64 64H64c-35.3 0-64-28.7-64-64V128C0 92.7 28.7 64 64 64h40 9.6C121 27.5 153.3 0 192 0s71 27.5 78.4 64H280zM64 112c-8.8 0-16 7.2-16 16V448c0 8.8 7.2 16 16 16H320c8.8 0 16-7.2 16-16V128c0-8.8-7.2-16-16-16H304v24c0 13.3-10.7 24-24 24H192 104c-13.3 0-24-10.7-24-24V112H64zm128-8a24 24 0 1 0 0-48 24 24 0 1 0 0 48z\",\n      },\n      direction: \"up\",\n      click: DualClick(copyImageToClipboard, () => {\n        popout_container();\n      }),\n    },\n    {\n      name: \"Download Image\",\n      icon: Plotly.Icons.camera,\n      direction: \"up\",\n      click: DualClick(saveImageToFile, () => {\n        popout_container({ cl: \"filesave\" });\n      }),\n    },\n  ]\n);\n"), HypertextLiteral.JavaScript("function getOffsetData(el) {\n  let cs = window.getComputedStyle(el, null);\n  const odata = {\n    padding: {\n      left: parseFloat(cs.paddingLeft),\n      right: parseFloat(cs.paddingRight),\n      top: parseFloat(cs.paddingTop),\n      bottom: parseFloat(cs.paddingBottom),\n      width: parseFloat(cs.paddingLeft) + parseFloat(cs.paddingRight),\n      height: parseFloat(cs.paddingTop) + parseFloat(cs.paddingBottom),\n    },\n    border: {\n      left: parseFloat(cs.borderLeftWidth),\n      right: parseFloat(cs.borderRightWidth),\n      top: parseFloat(cs.borderTopWidth),\n      bottom: parseFloat(cs.borderBottomWidth),\n      width: parseFloat(cs.borderLeftWidth) + parseFloat(cs.borderRightWidth),\n      height: parseFloat(cs.borderTopWidth) + parseFloat(cs.borderBottomWidth),\n    }\n  };\n  if (el === PLOT) {\n    // For the PLOT we also want to take into account the offset\n    odata.offset = {\n      top: PLOT.offsetParent == CONTAINER ? PLOT.offsetTop : 0,\n      left: PLOT.offsetParent == CONTAINER ? PLOT.offsetLeft : 0,\n    }\n  }\n  return odata;\n}\nfunction getSizeData() {\n  const data = {\n    plot_pad: getOffsetData(PLOT),\n    plot_rect: PLOT.getBoundingClientRect(),\n    container_pad: getOffsetData(CONTAINER),\n    container_rect: CONTAINER.getBoundingClientRect(),\n  };\n  return data;\n}\nfunction computeContainerSize({ width, height }, sizeData = getSizeData()) {\n  const computed_size = computePlotSize(sizeData);\n  const offsets = computed_size.offsets;\n\n  const plot_data = {\n    width: width ?? computed_size.width,\n    height: height ?? computed_size.height,\n  };\n\n  return {\n    width: (width ?? computed_size.width) + offsets.width,\n    height: (height ?? computed_size.height) + offsets.height,\n    noChange: width == computed_size.width && height == computed_size.height,\n  }\n}\n\n// This function will change the container size so that the resulting plot will be matching the provided specs\nfunction changeContainerSize({ width, height }, sizeData = getSizeData()) {\n  if (!CONTAINER.isPoppedOut()) {\n    console.log(\"Tried to change container size when not popped, ignoring\");\n    return;\n  }\n\n  const csz = computeContainerSize({ width, height }, sizeData);\n\n  if (csz.noChange) {\n    console.log(\"Size is the same as current, ignoring\");\n    return\n  }\n  // We are now going to set he width and height of the container\n  for (const key of [\"width\", \"height\"]) {\n    CONTAINER.style[key] = csz[key] + \"px\";\n  }\n}\n// We now create the function that will update the plot based on the values specified\nfunction updateFromHeader() {\n  const header_data = {\n    height: config_spans.height.ui_value,\n    width: config_spans.width.ui_value,\n  };\n  changeContainerSize(header_data);\n}\n// We assign this function to the onblur event of width and height\nif (firstRun) {\n  for (const container of Object.values(config_spans)) {\n    container.ui_span.onblur = (e) => {\n      container.ui_value = container.ui_span.textContent;\n      updateFromHeader();\n    };\n  }\n}\n// This function computes the plot size to use for relayout as a function of the container size\nfunction computePlotSize(data = getSizeData()) {\n  // Remove Padding\n  const { container_pad, plot_pad, container_rect } = data;\n  const offsets = {\n    width:\n      plot_pad.padding.width +\n      plot_pad.border.width +\n      plot_pad.offset.left +\n      container_pad.padding.width +\n      container_pad.border.width,\n    height:\n      plot_pad.padding.height +\n      plot_pad.border.height +\n      plot_pad.offset.top +\n      container_pad.padding.height +\n      container_pad.border.height,\n  };\n  const sz = {\n    width: Math.round(container_rect.width - offsets.width),\n    height: Math.round(container_rect.height - offsets.height),\n    offsets,\n  };\n  return sz;\n}\n\n// Create the resizeObserver to make the plot even more responsive! :magic:\nconst resizeObserver = new ResizeObserver((entries) => {\n  const sizeData = getSizeData();\n  const {container_rect, container_pad} = sizeData;\n  let plot_size = computePlotSize(sizeData);\n  // We save the height in the PLOT object\n  PLOT.container_height = container_rect.height;\n  // We deal with some stuff if the container is poppped\n  CLIPBOARD_HEADER.style.width = container_rect.width + \"px\";\n  CLIPBOARD_HEADER.style.left = container_rect.left + \"px\";\n  config_spans.height.ui_value = plot_size.height;\n  config_spans.width.ui_value = plot_size.width;\n  /* \n\t\tThe addition of the invalid argument `plutoresize` seems to fix the problem with calling `relayout` simply with `{autosize: true}` as update breaking mouse relayout events tracking. \n\t\tSee https://github.com/plotly/plotly.js/issues/6156 for details\n\t\t*/\n  let config = {\n    // If this is popped out, we ignore the original width/height\n    width: (CONTAINER.isPoppedOut() ? undefined : original_width) ?? plot_size.width,\n    height: (CONTAINER.isPoppedOut() ? undefined : original_height) ?? plot_size.height,\n    plutoresize: true,\n  };\n  Plotly.relayout(PLOT, config).then(() => {\n    if (remove_container_size && !CONTAINER.isPoppedOut()) {\n      // This is needed to avoid the first resize upon plot creation to already be without a fixed height\n      CONTAINER.style.height = \"\";\n      CONTAINER.style.width = \"\";\n      remove_container_size = false;\n    }\n  });\n});\n\nresizeObserver.observe(CONTAINER);\n"), HypertextLiteral.JavaScript("\nPlotly.react(PLOT, plot_obj).then(() => {\n\t// Assign the Plotly event listeners\n\tfor (const [key, listener_vec] of Object.entries(plotly_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.on(key, listener)\n\t\t}\n\t}\n\t// Assign the JS event listeners\n\tfor (const [key, listener_vec] of Object.entries(js_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.addEventListener(key, listener, {\n\t\t\t\tsignal: controller.signal\n\t\t\t})\n\t\t}\n\t}\n}\n)\n"), HypertextLiteral.JavaScript("\ninvalidation.then(() => {\n\t// Remove all plotly listeners\n\tPLOT.removeAllListeners()\n\t// Remove all JS listeners\n\tcontroller.abort()\n\t// Remove the resizeObserver\n\tresizeObserver.disconnect()\n})\n")])), nothing, nothing, nothing, nothing)

Resolución mediante regresión no lineal

Cargamos la biblioteca, creamos el modelo y realizamos el ajuste para la razón de amplitudes, lo que nos permitirá encontrar la ganancia y la constante de tiempo del proceso en cuestión:

using LsqFit

@. RAmodel_1(w, p) = p[1]/sqrt(1+p[2]^2*w^2)

fitRA1 = curve_fit(RAmodel_1, w_1, RA_1, [1.0,1.0]; autodiff=:forwarddiff)

LsqFit.LsqFitResult{Vector{Float64}, Vector{Float64}, Matrix{Float64}, Vector{Float64}, Vector{LsqFit.LMState{LsqFit.LevenbergMarquardt}}}([9.995973725031158, 0.10009388111275176], [-0.004031282340678288, 0.005848542992753281, 0.005473025093987616, -0.0037268863964108334, -0.006336056416909486, -0.0010083349439646838, -0.003507513194605849, -0.003172293161826545, 0.024903722436548925, -0.004277808779430181, -0.00883339307982478, -0.003019885143573653], [0.9999994990611245 -0.00010005343020183683; 0.9999874767539563 -0.002501245540604989; … ; 0.5543398531595183 -38.34806550782738; 0.4468779368307616 -35.71571644181666], true, Iter     Function value   Gradient norm 
------   --------------   --------------
, Float64[])

K_1 = fitRA1.param[1]
round(K_1, sigdigits=3)

10.0

T_1 = fitRA1.param[2]
round(T_1, sigdigits=3)

0.1

@. phimodel_1(w, p) = 180/pi*(atan(-T_1*w)-p[1]*w)

fitphi1 = curve_fit(phimodel_1, w_1, phi_1, [1.0]; autodiff=:forwarddiff)

LsqFit.LsqFitResult{Vector{Float64}, Vector{Float64}, Matrix{Float64}, Vector{Float64}, Vector{LsqFit.LMState{LsqFit.LevenbergMarquardt}}}([0.9999673701743539], [-0.00028864989389243423, -0.0014409512133504165, -0.002867539180766876, 0.00017121603750780423, 0.004222464622984035, -0.016112912019309533, -0.014652559968226342, -0.009137284454823202, -0.0059819548567929814, -0.007787855215156014, 0.006608111105038006, 0.015352123624552405], [-0.5729577951308232; -2.8647889756541165; … ; -859.4366926962348; -1145.9155902616465;;], true, Iter     Function value   Gradient norm 
------   --------------   --------------
, Float64[])

td_1 = fitphi1.param[1]
round(td_1, sigdigits=3)

1.0

Sistema 2

De nuevo, empezamos representando los datos del enunciado del problema:

w_2 = [0.01, 0.05, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.10, 1.50, 2.00, 5.00]
RA_2 = [5.00, 5.05, 5.20, 5.93, 7.68, 12.69, 25.00, 9.98, 5.00, 3.25, 2.20, 1.29, 0.62, 0.33, 0.05]
phi_2 = [-0.23, -1.13, -2.39, -5.44, -11.62, -23.96, -90.00, -151.39, -163.74, -168.10, -170.87, -173.46, -175.71, -176.95, -178.84];

scatter(w_2, RA_2, xscale=:log10, yscale=:log10,
    xlabel="ω₂", ylabel="RA₂", legend=false, dpi=350)

scatter(w_2, phi_2, xscale=:log10,
    xlabel="ω₂", ylabel="φ₂", legend=false, dpi=350)

El sistema 2 claramente es un sistema de segundo orden subamortiguado, solo hay que seguir las siguientes pistas:

1. El desfase tiende a -180° a medida que el valor de frecuencia angular aumenta.

2. El gráfico de razón de amplitudes del diagrama de Bode tiene un máximo que indica que se trata de un sistema subamortiguado.

3. El máximo de razón de amplitudes se produce para un retraso de -90°, lo que es propio de los sistemas de segundo orden.

Este problema nuevamente se puede resolver de cualquiera de las dos maneras para las que se ha resuelto el sistema 1. Si se realiza un ajuste no lineal para ajustar la razón de amplitudes respecto a la frecuencia angular, se obtiene:

# p[1]: Ganancia del sistema
# p[2]: Constante de tiempo
# p[3]: Coeficiente de amortiguamiento

@. RAmodel2(w, p) = p[1]/sqrt((1-p[2]^2*w^2)^2+(2*p[2]*p[3]*w)^2)

RAfit2 = curve_fit(RAmodel2, w_2, RA_2, [1.0, 1.0, 1.0]; autodiff=:forwarddiff)

LsqFit.LsqFitResult{Vector{Float64}, Vector{Float64}, Matrix{Float64}, Vector{Float64}, Vector{LsqFit.LMState{LsqFit.LevenbergMarquardt}}}([5.004332595589434, -1.9994457248500594, -0.10011895100290764], [0.006293864017719031, 0.0038200613266035077, 0.008199003709473018, 3.391806111441298e-5, 0.0027910040102687717, 0.0004748127835245697, -0.0012328551092473106, 0.016607118969471202, 0.009197149354097434, -0.104898297279989, 0.00744630658066292, 0.005617743325766034, 0.004173416606759073, 0.00334433049841637, 0.0005667789324355493], [1.00039191408461 -0.001962565079160098 0.0008021437527597949; 1.0098889242055542 -0.049980375755219526 0.02063015653783024; … ; 0.0666111462679777 0.35514143024987965 0.009472015501187174; 0.010104599957445384 0.05108144317264549 0.00020665174127284914], true, Iter     Function value   Gradient norm 
------   --------------   --------------
, Float64[])

Los parámetros obtenidos del sistema son:

• Ganancia:

K_2 = RAfit2.param[1]
round(K_2, sigdigits=3)

5.0

• Constante de tiempo:

T_2 = abs(RAfit2.param[2])
round(T_2, sigdigits=3)

2.0

• Coeficiente de amortiguamiento:

Z_2 = abs(RAfit2.param[3])
round(Z_2, sigdigits=3)

0.1

Para comprobar la calidad del ajuste representaremos la función de transferencia del proceso con los parámetros obtenidos más arriba junto con los datos experimentales:

G2(s) = K_2/(T_2^2*s^2+2*T_2*Z_2*s+1)

G2 (generic function with 1 method)

ClaseControl.bode(G2)

ClaseControl.Bode(PlutoPlotly.PlutoPlot(data: [
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis"
]

layout: "layout with fields margin, showlegend, template, xaxis1, xaxis2, yaxis1, and yaxis2"

, Dict{String, Vector{HypertextLiteral.JavaScript}}(), Dict{String, Vector{HypertextLiteral.JavaScript}}(), String[], PlutoPlotly.ScriptContents(HypertextLiteral.JavaScript[HypertextLiteral.JavaScript("// Flag to check if this cell was  manually ran or reactively ran\nconst firstRun = this ? false : true\nconst CONTAINER = this ?? html`<div class='plutoplotly-container'>`\nconst PLOT = CONTAINER.querySelector('.js-plotly-plot') ?? CONTAINER.appendChild(html`<div>`)\nconst parent = CONTAINER.parentElement\n// We use a controller to remove event listeners upon invalidation\nconst controller = new AbortController()\n// We have to add this to keep supporting @bind with the old API using PLOT\nPLOT.addEventListener('input', (e) => {\n\tCONTAINER.value = PLOT.value\n\tif (e.bubbles) {\n\t\treturn\n\t}\n\tCONTAINER.dispatchEvent(new CustomEvent('input'))\n}, { signal: controller.signal })\n"), HypertextLiteral.JavaScript("\t// This create the style subdiv on first run\n\tfirstRun && CONTAINER.appendChild(html`\n\t<style>\n\t.plutoplotly-container {\n\t\twidth: 100%;\n\t\theight: 100%;\n\t\tmin-height: 0;\n\t\tmin-width: 0;\n\t}\n\t.plutoplotly-container .js-plotly-plot .plotly div {\n\t\tmargin: 0 auto; // This centers the plot\n\t}\n\t.plutoplotly-container.popped-out {\n\t\toverflow: auto;\n\t\tz-index: 1000;\n\t\tposition: fixed;\n\t\tresize: both;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\tborder-top-left-radius: 0px;\n\t\tborder-top-right-radius: 0px;\n\t}\n\t.plutoplotly-clipboard-header {\n\t\tdisplay: flex;\n\t\tflex-flow: row wrap;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-top-left-radius: 12px;\n\t\tborder-top-right-radius: 12px;\n\t\tposition: fixed;\n\t\tz-index: 1001;\n\t\tcursor: move;\n\t\ttransform: translate(0px, -100%);\n\t\tpadding: 5px;\n\t}\n\t.plutoplotly-clipboard-header span {\n\t\tdisplay: inline-block;\n\t\tflex: 1\n\t}\n\t.plutoplotly-clipboard-header.hidden {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span {\n\t\tposition: relative;\n\t}\n\t.clipboard-value {\n\t\tpadding-right: 5px;\n\t\tpadding-left: 2px;\n\t\tcursor: text;\n\t}\n\t.clipboard-span.format {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span.filename {\n\t\tflex: 0 0 100%;\n\t\ttext-align: center;\n\t\tborder-top: 3px solid var(--kbd-border-color);\n\t\tmargin-top: 5px;\n\t\tdisplay: none;\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.filename {\n\t\tdisplay: inline-block;\n\t}\n\t.clipboard-value.filename {\n\t\tmargin-left: 3px;\n\t\ttext-align: left;\n\t\tmin-width: min(60%, min-content);\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.format {\n\t\tdisplay: inline-flex;\n\t}\n\t.clipboard-span.format .label {\n\t\tflex: 0 0 0;\n\t}\n\t.clipboard-value.format {\n\t\tposition: relative;\n\t\tflex: 1 0 auto;\n\t\tmin-width: 30px;\n\t\tmargin-right: 10px;\n\t}\n\tdiv.format-options {\n\t\tdisplay: inline-flex;\n\t\tflex-flow: column;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder-radius: 12px;\n\t\tpadding-left: 3px;\n\t\tz-index: 2000;\n\t}\n\tdiv.format-options:hover {\n\t\tcursor: pointer;\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tpadding: 3px;\n\t\ttransform: translate(-3px, -6px);\n\t}\n\tdiv.format-options .format-option {\n\t\tdisplay: none;\n\t}\n\tdiv.format-options:hover .format-option {\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:not(.selected) {\n\t\tmargin-top: 3px;\n\t}\n\tdiv.format-options .format-option.selected {\n\t\torder: -1;\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:hover {\n\t\tbackground-color: var(--kbd-border-color);\n\t}\n\tspan.config-value {\n\t\tfont-weight: normal;\n\t\tcolor: var(--pluto-output-color);\n\t\tdisplay: none;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\ttransform: translate(0px, calc(-100% - 10px));\n\t\tpadding: 5px;\n\t}\n\t.label {\n\t\tuser-select: none;\n\t}\n\t.label:hover span.config-value {\n\t\tdisplay: inline-block;\n\t\tmin-width: 150px;\n\t}\n\t.clipboard-span.matching-config .label {\n\t\tcolor: var(--cm-macro-color);\n\t\tfont-weight: bold;\n\t}\n\t.clipboard-span.different-config .label {\n\t\tcolor: var(--cm-tag-color);\n\t\tfont-weight: bold;\n\t}\n</style>\n`)\n"), HypertextLiteral.JavaScript("let original_height = plot_obj.layout.height\nlet original_width = plot_obj.layout.width\n// For the height we have to also put a fixed value in case the plot is put on a non-fixed-size container (like the default wrapper)\n// We define a variable to check whether we still have to remove the fixed height\nlet remove_container_size = firstRun\nlet container_height = original_height ?? PLOT.container_height ?? 400\nCONTAINER.style.height = container_height + 'px'\n"), HypertextLiteral.JavaScript("// We create a Promise version of setTimeout\nfunction delay(ms) {\n  return new Promise((resolve) => setTimeout(resolve, ms));\n}\n\n// We import interact for dragging/resizing\nconst { default: interact } = await import('https://esm.sh/interactjs@1.10.19')\n\n\nfunction getImageOptions() {\n  const o = plot_obj.config.toImageButtonOptions ?? {};\n  return {\n    format: o.format ?? \"png\",\n    width: o.width ?? original_width,\n    height: o.height ?? original_height,\n    scale: o.scale ?? 1,\n    filename: o.filename ?? \"newplot\",\n  };\n}\n\nconst CLIPBOARD_HEADER =\n  CONTAINER.querySelector(\".plutoplotly-clipboard-header\") ??\n  CONTAINER.insertAdjacentElement(\n    \"afterbegin\",\n    html`<div class=\"plutoplotly-clipboard-header hidden\">\n      <span class=\"clipboard-span format\"\n        ><span class=\"label\">Format:</span\n        ><span class=\"clipboard-value format\"></span\n      ></span>\n      <span class=\"clipboard-span width\"\n        ><span class=\"label\">Width:</span\n        ><span class=\"clipboard-value width\"></span>px</span\n      >\n      <span class=\"clipboard-span height\"\n        ><span class=\"label\">Height:</span\n        ><span class=\"clipboard-value height\"></span>px</span\n      >\n      <span class=\"clipboard-span scale\"\n        ><span class=\"label\">Scale:</span\n        ><span class=\"clipboard-value scale\"></span\n      ></span>\n      <button class=\"clipboard-span set\">Set</button>\n      <button class=\"clipboard-span unset\">Unset</button>\n      <span class=\"clipboard-span filename\"\n        ><span class=\"label\">Filename:</span\n        ><span class=\"clipboard-value filename\"></span\n      ></span>\n    </div>`\n  );\n\nfunction checkConfigSync(container) {\n  const valid_classes = [\n    \"missing-config\",\n    \"matching-config\",\n    \"different-config\",\n  ];\n  function setClass(cl) {\n    for (const name of valid_classes) {\n      container.classList.toggle(name, name == cl);\n    }\n  }\n  // We use the custom getters we'll set up in the container\n  const { ui_value, config_value, config_span, key } = container;\n  if (config_value === undefined) {\n    setClass(\"missing-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> is not present in the config.`;\n  } else if (ui_value == config_value) {\n    setClass(\"matching-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has the same value in the config and in the header.`;\n  } else {\n    setClass(\"different-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has a different value (<em>\${config_value}</em>) in the config.`;\n  }\n  // Add info about setting and unsetting\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click on the label <em><b>once</b></em> to set the current UI value in the config.`\n  );\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click <em><b>twice</b></em> to remove this key from the config.`\n  );\n}\n\nconst valid_formats = [\"png\", \"svg\", \"webp\", \"jpeg\", \"full-json\"];\nfunction initializeUIValueSpan(span, key, value) {\n  const container = span.closest(\".clipboard-span\");\n  span.contentEditable = key === \"format\" ? \"false\" : \"true\";\n  let parse = (x) => x;\n  let update = (x) => (span.textContent = x);\n  if (key === \"width\" || key === \"height\") {\n    parse = (x) => Math.round(parseFloat(x));\n  } else if (key === \"scale\") {\n    parse = parseFloat;\n  } else if (key === \"format\") {\n    // We remove contentEditable\n    span.contentEditable = \"false\";\n    // Here we first add the subspans for each option\n    const opts_div = span.appendChild(html`<div class=\"format-options\"></div>`);\n    for (const fmt of valid_formats) {\n      const opt = opts_div.appendChild(\n        html`<span class=\"format-option \${fmt}\">\${fmt}</span>`\n      );\n      opt.onclick = (e) => {\n        span.value = opt.textContent;\n      };\n    }\n    parse = (x) => {\n      return valid_formats.includes(x) ? x : localValue;\n    };\n    update = (x) => {\n      for (const opt of opts_div.children) {\n        opt.classList.toggle(\"selected\", opt.textContent === x);\n      }\n    };\n  } else {\n    // We only have filename here\n  }\n  let localValue;\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return localValue;\n    },\n    set: (val) => {\n      if (val !== \"\") {\n        localValue = parse(val);\n      }\n      update(localValue);\n      checkConfigSync(container);\n    },\n  });\n  // We also assign a listener so that the editable is blurred when enter is pressed\n  span.onkeydown = (e) => {\n    if (e.keyCode === 13) {\n      e.preventDefault();\n      span.blur();\n    }\n  };\n  span.value = value;\n}\n\nfunction initializeConfigValueSpan(span, key) {\n  // Here we mostly want to define the setter and getter\n  const container = span.closest(\".clipboard-span\");\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return plot_obj.config.toImageButtonOptions[key];\n    },\n    set: (val) => {\n      // if undefined is passed, we remove the entry from the options\n      if (val === undefined) {\n        delete plot_obj.config.toImageButtonOptions[key];\n      } else {\n        plot_obj.config.toImageButtonOptions[key] = val;\n      }\n      checkConfigSync(container);\n    },\n  });\n}\n\nconst config_spans = {};\nfor (const [key, value] of Object.entries(getImageOptions())) {\n  const container = CLIPBOARD_HEADER.querySelector(`.clipboard-span.\${key}`);\n  const label = container.querySelector(\".label\");\n  // We give the label a function that on single click will set the current value and with double click will unset it\n  label.onclick = DualClick(\n    () => {\n      container.config_value = container.ui_value;\n    },\n    (e) => {\n      console.log(\"e\", e);\n      e.preventDefault();\n      container.config_value = undefined;\n    }\n  );\n  const ui_value_span = container.querySelector(\".clipboard-value\");\n  const config_value_span =\n    container.querySelector(\".config-value\") ??\n    label.insertAdjacentElement(\n      \"afterbegin\",\n      html`<span class=\"config-value\"></span>`\n    );\n  // Assing the two spans as properties of the containing span\n  container.ui_span = ui_value_span;\n  container.config_span = config_value_span;\n  container.key = key;\n  config_spans[key] = container;\n  if (firstRun) {\n    plot_obj.config.toImageButtonOptions =\n      plot_obj.config.toImageButtonOptions ?? {};\n    // We do the initialization of the value span\n    initializeUIValueSpan(ui_value_span, key, value);\n    // Then we initialize the config value\n    initializeConfigValueSpan(config_value_span, key);\n    // We put some convenience getters/setters\n    // ui_value forward\n    Object.defineProperty(container, \"ui_value\", {\n      get: () => ui_value_span.value,\n      set: (val) => {\n        ui_value_span.value = val;\n      },\n    });\n    // config_value forward\n    Object.defineProperty(container, \"config_value\", {\n      get: () => config_value_span.value,\n      set: (val) => {\n        config_value_span.value = val;\n      },\n    });\n  }\n}\n\n// These objects will contain the default value\n\n// This code updates the image options in the PLOT config with the provided ones\nfunction setImageOptions(o) {\n  for (const [key, container] of Object.entries(config_spans)) {\n    container.config_value = o[key];\n  }\n}\nfunction unsetImageOptions() {\n  setImageOptions({});\n}\n\nconst set_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.set\");\nconst unset_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.unset\");\nif (firstRun) {\n  set_button.onclick = (e) => {\n    for (const container of Object.values(config_spans)) {\n      container.config_value = container.ui_value;\n    }\n  };\n  unset_button.onclick = unsetImageOptions;\n}\n\n// We add a function to check if the clipboard is popped out\nCONTAINER.isPoppedOut = () => {\n  return CONTAINER.classList.contains(\"popped-out\");\n};\n\nCLIPBOARD_HEADER.onmousedown = function (event) {\n  if (event.target.matches(\"span.clipboard-value\")) {\n    console.log(\"We don't move!\");\n    return;\n  }\n  const start = {\n    left: parseFloat(CONTAINER.style.left),\n    top: parseFloat(CONTAINER.style.top),\n    X: event.pageX,\n    Y: event.pageY,\n  };\n  function moveAt(event, start) {\n    const top = event.pageY - start.Y + start.top + \"px\";\n    const left = event.pageX - start.X + start.left + \"px\";\n    CLIPBOARD_HEADER.style.left = left;\n    CONTAINER.style.left = left;\n    CONTAINER.style.top = top;\n  }\n\n  // move our absolutely positioned ball under the pointer\n  moveAt(event, start);\n  function onMouseMove(event) {\n    moveAt(event, start);\n  }\n\n  // We use this to remove the mousemove when clicking outside of the container\n  const controller = new AbortController();\n\n  // move the container on mousemove\n  document.addEventListener(\"mousemove\", onMouseMove, {\n    signal: controller.signal,\n  });\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        cleanUp();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n\n  function cleanUp() {\n    console.log(\"cleaning up the plot move listener\");\n    controller.abort();\n    CLIPBOARD_HEADER.onmouseup = null;\n  }\n\n  // (3) drop the ball, remove unneeded handlers\n  CLIPBOARD_HEADER.onmouseup = cleanUp;\n};\n\nfunction sendToClipboard(blob) {\n  if (!navigator.clipboard) {\n    alert(\n      \"The Clipboard API does not seem to be available, make sure the Pluto notebook is being used from either localhost or an https source.\"\n    );\n  }\n  navigator.clipboard\n    .write([\n      new ClipboardItem({\n        // The key is determined dynamically based on the blob's type.\n        [blob.type]: blob,\n      }),\n    ])\n    .then(\n      function () {\n        console.log(\"Async: Copying to clipboard was successful!\");\n      },\n      function (err) {\n        console.error(\"Async: Could not copy text: \", err);\n      }\n    );\n}\n\nfunction copyImageToClipboard() {\n  // We extract the image options from the provided parameters (if they exist)\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key. We also ignore format because the clipboard only supports png.\n    if (val === undefined || key === \"format\") {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.toImage(PLOT, config).then(function (dataUrl) {\n    fetch(dataUrl)\n      .then((res) => res.blob())\n      .then((blob) => {\n        const paste_receiver = document.querySelector('paste-receiver.plutoplotly')\n        if (paste_receiver) {\n          paste_receiver.attachImage(dataUrl, CONTAINER)\n        }\n        sendToClipboard(blob)\n      });\n  });\n}\n\nfunction saveImageToFile() {\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key.\n    if (val === undefined) {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.downloadImage(PLOT, config);\n}\n\nlet container_rect = { width: 0, height: 0, top: 0, left: 0 };\nfunction unpop_container(cl) {\n  CONTAINER.classList.toggle(\"popped-out\", false);\n  CONTAINER.classList.toggle(cl, false);\n  // We fix the height back to the value it had before popout, also setting the flag to signal that upon first resize we remove the fixed inline-style\n  CONTAINER.style.height = container_rect.height + \"px\";\n  remove_container_size = true;\n  // We set the other fixed inline-styles to null\n  CONTAINER.style.width = \"\";\n  CONTAINER.style.top = \"\";\n  CONTAINER.style.left = \"\";\n  // We also remove the CLIPBOARD_HEADER\n  CLIPBOARD_HEADER.style.width = \"\";\n  CLIPBOARD_HEADER.style.left = \"\";\n  // Finally we remove the hidden class to the header\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", true);\n  return;\n}\nfunction popout_container(opts) {\n  const cl = opts?.cl;\n  const target_container_size = opts?.target_container_size ?? {};\n  const target_plot_size = opts?.target_plot_size ?? {};\n  if (CONTAINER.isPoppedOut()) {\n    return unpop_container(cl);\n  }\n  CONTAINER.classList.toggle(cl, cl === undefined ? false : true);\n  // We extract the current size of the container, save them and fix them\n  const { width, height, top, left } = CONTAINER.getBoundingClientRect();\n  container_rect = { width, height, top, left };\n  // We save the current plot size before we pop as it will fill the screen\n  const current_plot_size = {\n    width: PLOT._fullLayout.width,\n    height: PLOT._fullLayout.height,\n  };\n  // We have to save the pad data before popping so we can resize precisely\n  const pad = {};\n  pad.unpopped = getSizeData().container_pad;\n  CONTAINER.classList.toggle(\"popped-out\", true);\n  pad.popped = getSizeData().container_pad;\n  // We do top and left based on the current rect\n  for (const key of [\"top\", \"left\"]) {\n    const start_val = target_container_size[key] ?? container_rect[key];\n    let offset = 0;\n    for (const kind of [\"padding\", \"border\"]) {\n      offset += pad.popped[kind][key] - pad.unpopped[kind][key];\n    }\n    CONTAINER.style[key] = start_val - offset + \"px\";\n    if (key === \"left\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  // We compute the width and height depending on eventual config data\n  const csz = computeContainerSize({\n    width:\n      target_plot_size.width ??\n      config_spans.width.config_value ??\n      current_plot_size.width,\n    height:\n      target_plot_size.height ??\n      config_spans.height.config_value ??\n      current_plot_size.height,\n  });\n  for (const key of [\"width\", \"height\"]) {\n    const val = target_container_size[key] ?? csz[key];\n    CONTAINER.style[key] = val + \"px\";\n    if (key === \"width\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", false);\n  const controller = new AbortController();\n\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        unpop_container();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n}\n\nCONTAINER.popOut = popout_container;\n\nfunction DualClick(single_func, dbl_func) {\n  let nclicks = 0;\n  return function (...args) {\n    nclicks += 1;\n    if (nclicks > 1) {\n      dbl_func(...args);\n      nclicks = 0;\n    } else {\n      delay(300).then(() => {\n        if (nclicks == 1) {\n          single_func(...args);\n        }\n        nclicks = 0;\n      });\n    }\n  };\n}\n\n// We remove the default download image button\nplot_obj.config.modeBarButtonsToRemove = _.union(\n  plot_obj.config.modeBarButtonsToRemove,\n  [\"toImage\"]\n);\n// We add the custom button to the modebar\nplot_obj.config.modeBarButtonsToAdd = _.union(\n  plot_obj.config.modeBarButtonsToAdd,\n  [\n    {\n      name: \"Copy PNG to Clipboard\",\n      icon: {\n        height: 520,\n        width: 520,\n        path: \"M280 64h40c35.3 0 64 28.7 64 64V448c0 35.3-28.7 64-64 64H64c-35.3 0-64-28.7-64-64V128C0 92.7 28.7 64 64 64h40 9.6C121 27.5 153.3 0 192 0s71 27.5 78.4 64H280zM64 112c-8.8 0-16 7.2-16 16V448c0 8.8 7.2 16 16 16H320c8.8 0 16-7.2 16-16V128c0-8.8-7.2-16-16-16H304v24c0 13.3-10.7 24-24 24H192 104c-13.3 0-24-10.7-24-24V112H64zm128-8a24 24 0 1 0 0-48 24 24 0 1 0 0 48z\",\n      },\n      direction: \"up\",\n      click: DualClick(copyImageToClipboard, () => {\n        popout_container();\n      }),\n    },\n    {\n      name: \"Download Image\",\n      icon: Plotly.Icons.camera,\n      direction: \"up\",\n      click: DualClick(saveImageToFile, () => {\n        popout_container({ cl: \"filesave\" });\n      }),\n    },\n  ]\n);\n"), HypertextLiteral.JavaScript("function getOffsetData(el) {\n  let cs = window.getComputedStyle(el, null);\n  const odata = {\n    padding: {\n      left: parseFloat(cs.paddingLeft),\n      right: parseFloat(cs.paddingRight),\n      top: parseFloat(cs.paddingTop),\n      bottom: parseFloat(cs.paddingBottom),\n      width: parseFloat(cs.paddingLeft) + parseFloat(cs.paddingRight),\n      height: parseFloat(cs.paddingTop) + parseFloat(cs.paddingBottom),\n    },\n    border: {\n      left: parseFloat(cs.borderLeftWidth),\n      right: parseFloat(cs.borderRightWidth),\n      top: parseFloat(cs.borderTopWidth),\n      bottom: parseFloat(cs.borderBottomWidth),\n      width: parseFloat(cs.borderLeftWidth) + parseFloat(cs.borderRightWidth),\n      height: parseFloat(cs.borderTopWidth) + parseFloat(cs.borderBottomWidth),\n    }\n  };\n  if (el === PLOT) {\n    // For the PLOT we also want to take into account the offset\n    odata.offset = {\n      top: PLOT.offsetParent == CONTAINER ? PLOT.offsetTop : 0,\n      left: PLOT.offsetParent == CONTAINER ? PLOT.offsetLeft : 0,\n    }\n  }\n  return odata;\n}\nfunction getSizeData() {\n  const data = {\n    plot_pad: getOffsetData(PLOT),\n    plot_rect: PLOT.getBoundingClientRect(),\n    container_pad: getOffsetData(CONTAINER),\n    container_rect: CONTAINER.getBoundingClientRect(),\n  };\n  return data;\n}\nfunction computeContainerSize({ width, height }, sizeData = getSizeData()) {\n  const computed_size = computePlotSize(sizeData);\n  const offsets = computed_size.offsets;\n\n  const plot_data = {\n    width: width ?? computed_size.width,\n    height: height ?? computed_size.height,\n  };\n\n  return {\n    width: (width ?? computed_size.width) + offsets.width,\n    height: (height ?? computed_size.height) + offsets.height,\n    noChange: width == computed_size.width && height == computed_size.height,\n  }\n}\n\n// This function will change the container size so that the resulting plot will be matching the provided specs\nfunction changeContainerSize({ width, height }, sizeData = getSizeData()) {\n  if (!CONTAINER.isPoppedOut()) {\n    console.log(\"Tried to change container size when not popped, ignoring\");\n    return;\n  }\n\n  const csz = computeContainerSize({ width, height }, sizeData);\n\n  if (csz.noChange) {\n    console.log(\"Size is the same as current, ignoring\");\n    return\n  }\n  // We are now going to set he width and height of the container\n  for (const key of [\"width\", \"height\"]) {\n    CONTAINER.style[key] = csz[key] + \"px\";\n  }\n}\n// We now create the function that will update the plot based on the values specified\nfunction updateFromHeader() {\n  const header_data = {\n    height: config_spans.height.ui_value,\n    width: config_spans.width.ui_value,\n  };\n  changeContainerSize(header_data);\n}\n// We assign this function to the onblur event of width and height\nif (firstRun) {\n  for (const container of Object.values(config_spans)) {\n    container.ui_span.onblur = (e) => {\n      container.ui_value = container.ui_span.textContent;\n      updateFromHeader();\n    };\n  }\n}\n// This function computes the plot size to use for relayout as a function of the container size\nfunction computePlotSize(data = getSizeData()) {\n  // Remove Padding\n  const { container_pad, plot_pad, container_rect } = data;\n  const offsets = {\n    width:\n      plot_pad.padding.width +\n      plot_pad.border.width +\n      plot_pad.offset.left +\n      container_pad.padding.width +\n      container_pad.border.width,\n    height:\n      plot_pad.padding.height +\n      plot_pad.border.height +\n      plot_pad.offset.top +\n      container_pad.padding.height +\n      container_pad.border.height,\n  };\n  const sz = {\n    width: Math.round(container_rect.width - offsets.width),\n    height: Math.round(container_rect.height - offsets.height),\n    offsets,\n  };\n  return sz;\n}\n\n// Create the resizeObserver to make the plot even more responsive! :magic:\nconst resizeObserver = new ResizeObserver((entries) => {\n  const sizeData = getSizeData();\n  const {container_rect, container_pad} = sizeData;\n  let plot_size = computePlotSize(sizeData);\n  // We save the height in the PLOT object\n  PLOT.container_height = container_rect.height;\n  // We deal with some stuff if the container is poppped\n  CLIPBOARD_HEADER.style.width = container_rect.width + \"px\";\n  CLIPBOARD_HEADER.style.left = container_rect.left + \"px\";\n  config_spans.height.ui_value = plot_size.height;\n  config_spans.width.ui_value = plot_size.width;\n  /* \n\t\tThe addition of the invalid argument `plutoresize` seems to fix the problem with calling `relayout` simply with `{autosize: true}` as update breaking mouse relayout events tracking. \n\t\tSee https://github.com/plotly/plotly.js/issues/6156 for details\n\t\t*/\n  let config = {\n    // If this is popped out, we ignore the original width/height\n    width: (CONTAINER.isPoppedOut() ? undefined : original_width) ?? plot_size.width,\n    height: (CONTAINER.isPoppedOut() ? undefined : original_height) ?? plot_size.height,\n    plutoresize: true,\n  };\n  Plotly.relayout(PLOT, config).then(() => {\n    if (remove_container_size && !CONTAINER.isPoppedOut()) {\n      // This is needed to avoid the first resize upon plot creation to already be without a fixed height\n      CONTAINER.style.height = \"\";\n      CONTAINER.style.width = \"\";\n      remove_container_size = false;\n    }\n  });\n});\n\nresizeObserver.observe(CONTAINER);\n"), HypertextLiteral.JavaScript("\nPlotly.react(PLOT, plot_obj).then(() => {\n\t// Assign the Plotly event listeners\n\tfor (const [key, listener_vec] of Object.entries(plotly_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.on(key, listener)\n\t\t}\n\t}\n\t// Assign the JS event listeners\n\tfor (const [key, listener_vec] of Object.entries(js_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.addEventListener(key, listener, {\n\t\t\t\tsignal: controller.signal\n\t\t\t})\n\t\t}\n\t}\n}\n)\n"), HypertextLiteral.JavaScript("\ninvalidation.then(() => {\n\t// Remove all plotly listeners\n\tPLOT.removeAllListeners()\n\t// Remove all JS listeners\n\tcontroller.abort()\n\t// Remove the resizeObserver\n\tresizeObserver.disconnect()\n})\n")])), nothing, nothing, nothing, nothing)

Sistema 3

En este caso se supondrá que se trata de un sistema de segundo orden sobreamortiguado con retraso:

w_3 = [0.01, 0.02, 0.10, 0.30, 0.50, 0.70, 1.00, 1.50, 2.00, 2.50, 3.00, 4.00, 8.00, 10.00, 20.00]
RA_3 = [17, 16.99, 16.67, 14.42, 11.66, 9.33, 6.80, 4.30, 2.92, 2.07, 1.55, 0.94, 0.26, 0.17, 0.04]
phi_3 = [-1.49, -2.98, -14.75, -41.21, -61.90, -77.76, -95.73, -117.03, -132.42, -144.53, -154.04, -169.23, -208.22, -223.12, -287.45];

scatter(w_3, RA_3, xscale=:log10, yscale=:log10,
    xlabel="ω₃", ylabel="RA₃", legend=false, dpi=350)

scatter(w_3, phi_3, xscale=:log10,
    xlabel="ω₃", ylabel="φ₃", legend=false, dpi=350)

En primer lugar, se obtendrá la ganancia, la constante de tiempo y el coeficiente de amortiguamiento del sistema ajustando la razón de amplitudes:

@. RAmodel3(w, p) = p[1]/sqrt((1-p[2]^2*w^2)^2+(2*p[2]*p[3]*w)^2)

RAfit3 = curve_fit(RAmodel3, w_3, RA_3, [1.0, 1.0, 1.0]; autodiff=:forwarddiff)

LsqFit.LsqFitResult{Vector{Float64}, Vector{Float64}, Matrix{Float64}, Vector{Float64}, Vector{LsqFit.LMState{LsqFit.LevenbergMarquardt}}}([17.00894104880903, -1.0010573200438633, -1.249495468209743], [0.005324369092630121, 0.004487134540500648, -0.012488268917962841, 0.0016676885911977024, 0.004609780915256323, -0.002918241632684726, -0.0008676683175261601, -0.0012069536891559096, -0.006567027601693809, 0.010846511724610597, -0.0013537504702396674, 0.0018252109282144158, -0.003189290657039101, -0.003762198615903295, 0.0022095343682418736], [0.9997873659679328 0.007223585567908273 0.008513590895022023; 0.9991502166873848 0.028843220371402058 0.03398929807924029; … ; 0.009773553856589838 0.3253448423961448 0.007953300199332608; 0.002481608599096026 0.08388754142770173 0.0005207744768818782], true, Iter     Function value   Gradient norm 
------   --------------   --------------
, Float64[])

Se encuentran los siguientes parámetros del proceso:

• Ganancia:

K_3 = RAfit3.param[1]
round(K_3, sigdigits=3)

17.0

• Constante de tiempo: Aunque el valor del ajuste es negativo, este valor no tiene sentido físico, ya que debe ser un valor positivo. Se puede tomar el valor positivo sin problema, ya que en el modelo la constante de tiempo aparece elevada al cuadrado, por lo que no afecta al ajuste el signo de este parámetro:

T_3 = RAfit3.param[2]
round(T_3, sigdigits=3)

-1.0

• Coeficiente de amortiguamiento: Ocurre con el signo el mismo problema que en el caso anterior:

Z_3 = RAfit3.param[3]
round(Z_3, sigdigits=3)

-1.25

Utilizando los parámetros obtenidos con el ajuste anterior y los datos de desfase se puede encontrar el retraso:

@. phimodel3(w, p) = 180/pi*(atan(-2*Z_3*T_3*w/(1-T_3^2*w^2))-p[1]*w)-180*(w>0.7)

phimodel3 (generic function with 1 method)

phifit3 = curve_fit(phimodel3, w_3, phi_3, [1.0]; autodiff=:forwarddiff)

LsqFit.LsqFitResult{Vector{Float64}, Vector{Float64}, Matrix{Float64}, Vector{Float64}, Vector{LsqFit.LMState{LsqFit.LevenbergMarquardt}}}([0.09997274324626008], [-0.0004550599482033846, 2.0964885032004332e-5, -0.004315113442558527, -0.027178087348723068, -0.03458157978677434, -0.04330122807311909, -0.04647418863925168, -0.05115281559162099, -0.054517095713464414, 0.12713475044066058, -0.04095240925985877, -0.03432719945126905, -0.01622343255735359, -0.007966020552117925, 0.0220102568649736], [-0.5729577951308232; -1.1459155902616465; … ; -572.9577951308232; -1145.9155902616465;;], true, Iter     Function value   Gradient norm 
------   --------------   --------------
, Float64[])

td_3 = phifit3.param[1]
round(td_3, sigdigits=3)

0.1

G3(s) = K_3/(T_3^2*s^2+2*T_3*Z_3*s+1)*exp(-td_3*s)

G3 (generic function with 1 method)

ClaseControl.bode(G3)

ClaseControl.Bode(PlutoPlotly.PlutoPlot(data: [
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, x, xaxis, y, and yaxis",
  "scatter with fields type, xaxis, and yaxis",
  "scatter with fields type, xaxis, and yaxis"
]

layout: "layout with fields margin, showlegend, template, xaxis1, xaxis2, yaxis1, and yaxis2"

, Dict{String, Vector{HypertextLiteral.JavaScript}}(), Dict{String, Vector{HypertextLiteral.JavaScript}}(), String[], PlutoPlotly.ScriptContents(HypertextLiteral.JavaScript[HypertextLiteral.JavaScript("// Flag to check if this cell was  manually ran or reactively ran\nconst firstRun = this ? false : true\nconst CONTAINER = this ?? html`<div class='plutoplotly-container'>`\nconst PLOT = CONTAINER.querySelector('.js-plotly-plot') ?? CONTAINER.appendChild(html`<div>`)\nconst parent = CONTAINER.parentElement\n// We use a controller to remove event listeners upon invalidation\nconst controller = new AbortController()\n// We have to add this to keep supporting @bind with the old API using PLOT\nPLOT.addEventListener('input', (e) => {\n\tCONTAINER.value = PLOT.value\n\tif (e.bubbles) {\n\t\treturn\n\t}\n\tCONTAINER.dispatchEvent(new CustomEvent('input'))\n}, { signal: controller.signal })\n"), HypertextLiteral.JavaScript("\t// This create the style subdiv on first run\n\tfirstRun && CONTAINER.appendChild(html`\n\t<style>\n\t.plutoplotly-container {\n\t\twidth: 100%;\n\t\theight: 100%;\n\t\tmin-height: 0;\n\t\tmin-width: 0;\n\t}\n\t.plutoplotly-container .js-plotly-plot .plotly div {\n\t\tmargin: 0 auto; // This centers the plot\n\t}\n\t.plutoplotly-container.popped-out {\n\t\toverflow: auto;\n\t\tz-index: 1000;\n\t\tposition: fixed;\n\t\tresize: both;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\tborder-top-left-radius: 0px;\n\t\tborder-top-right-radius: 0px;\n\t}\n\t.plutoplotly-clipboard-header {\n\t\tdisplay: flex;\n\t\tflex-flow: row wrap;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-top-left-radius: 12px;\n\t\tborder-top-right-radius: 12px;\n\t\tposition: fixed;\n\t\tz-index: 1001;\n\t\tcursor: move;\n\t\ttransform: translate(0px, -100%);\n\t\tpadding: 5px;\n\t}\n\t.plutoplotly-clipboard-header span {\n\t\tdisplay: inline-block;\n\t\tflex: 1\n\t}\n\t.plutoplotly-clipboard-header.hidden {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span {\n\t\tposition: relative;\n\t}\n\t.clipboard-value {\n\t\tpadding-right: 5px;\n\t\tpadding-left: 2px;\n\t\tcursor: text;\n\t}\n\t.clipboard-span.format {\n\t\tdisplay: none;\n\t}\n\t.clipboard-span.filename {\n\t\tflex: 0 0 100%;\n\t\ttext-align: center;\n\t\tborder-top: 3px solid var(--kbd-border-color);\n\t\tmargin-top: 5px;\n\t\tdisplay: none;\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.filename {\n\t\tdisplay: inline-block;\n\t}\n\t.clipboard-value.filename {\n\t\tmargin-left: 3px;\n\t\ttext-align: left;\n\t\tmin-width: min(60%, min-content);\n\t}\n\t.plutoplotly-container.filesave .clipboard-span.format {\n\t\tdisplay: inline-flex;\n\t}\n\t.clipboard-span.format .label {\n\t\tflex: 0 0 0;\n\t}\n\t.clipboard-value.format {\n\t\tposition: relative;\n\t\tflex: 1 0 auto;\n\t\tmin-width: 30px;\n\t\tmargin-right: 10px;\n\t}\n\tdiv.format-options {\n\t\tdisplay: inline-flex;\n\t\tflex-flow: column;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder-radius: 12px;\n\t\tpadding-left: 3px;\n\t\tz-index: 2000;\n\t}\n\tdiv.format-options:hover {\n\t\tcursor: pointer;\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tpadding: 3px;\n\t\ttransform: translate(-3px, -6px);\n\t}\n\tdiv.format-options .format-option {\n\t\tdisplay: none;\n\t}\n\tdiv.format-options:hover .format-option {\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:not(.selected) {\n\t\tmargin-top: 3px;\n\t}\n\tdiv.format-options .format-option.selected {\n\t\torder: -1;\n\t\tdisplay: inline-block;\n\t}\n\t.format-option:hover {\n\t\tbackground-color: var(--kbd-border-color);\n\t}\n\tspan.config-value {\n\t\tfont-weight: normal;\n\t\tcolor: var(--pluto-output-color);\n\t\tdisplay: none;\n\t\tposition: absolute;\n\t\tbackground: var(--main-bg-color);\n\t\tborder: 3px solid var(--kbd-border-color);\n\t\tborder-radius: 12px;\n\t\ttransform: translate(0px, calc(-100% - 10px));\n\t\tpadding: 5px;\n\t}\n\t.label {\n\t\tuser-select: none;\n\t}\n\t.label:hover span.config-value {\n\t\tdisplay: inline-block;\n\t\tmin-width: 150px;\n\t}\n\t.clipboard-span.matching-config .label {\n\t\tcolor: var(--cm-macro-color);\n\t\tfont-weight: bold;\n\t}\n\t.clipboard-span.different-config .label {\n\t\tcolor: var(--cm-tag-color);\n\t\tfont-weight: bold;\n\t}\n</style>\n`)\n"), HypertextLiteral.JavaScript("let original_height = plot_obj.layout.height\nlet original_width = plot_obj.layout.width\n// For the height we have to also put a fixed value in case the plot is put on a non-fixed-size container (like the default wrapper)\n// We define a variable to check whether we still have to remove the fixed height\nlet remove_container_size = firstRun\nlet container_height = original_height ?? PLOT.container_height ?? 400\nCONTAINER.style.height = container_height + 'px'\n"), HypertextLiteral.JavaScript("// We create a Promise version of setTimeout\nfunction delay(ms) {\n  return new Promise((resolve) => setTimeout(resolve, ms));\n}\n\n// We import interact for dragging/resizing\nconst { default: interact } = await import('https://esm.sh/interactjs@1.10.19')\n\n\nfunction getImageOptions() {\n  const o = plot_obj.config.toImageButtonOptions ?? {};\n  return {\n    format: o.format ?? \"png\",\n    width: o.width ?? original_width,\n    height: o.height ?? original_height,\n    scale: o.scale ?? 1,\n    filename: o.filename ?? \"newplot\",\n  };\n}\n\nconst CLIPBOARD_HEADER =\n  CONTAINER.querySelector(\".plutoplotly-clipboard-header\") ??\n  CONTAINER.insertAdjacentElement(\n    \"afterbegin\",\n    html`<div class=\"plutoplotly-clipboard-header hidden\">\n      <span class=\"clipboard-span format\"\n        ><span class=\"label\">Format:</span\n        ><span class=\"clipboard-value format\"></span\n      ></span>\n      <span class=\"clipboard-span width\"\n        ><span class=\"label\">Width:</span\n        ><span class=\"clipboard-value width\"></span>px</span\n      >\n      <span class=\"clipboard-span height\"\n        ><span class=\"label\">Height:</span\n        ><span class=\"clipboard-value height\"></span>px</span\n      >\n      <span class=\"clipboard-span scale\"\n        ><span class=\"label\">Scale:</span\n        ><span class=\"clipboard-value scale\"></span\n      ></span>\n      <button class=\"clipboard-span set\">Set</button>\n      <button class=\"clipboard-span unset\">Unset</button>\n      <span class=\"clipboard-span filename\"\n        ><span class=\"label\">Filename:</span\n        ><span class=\"clipboard-value filename\"></span\n      ></span>\n    </div>`\n  );\n\nfunction checkConfigSync(container) {\n  const valid_classes = [\n    \"missing-config\",\n    \"matching-config\",\n    \"different-config\",\n  ];\n  function setClass(cl) {\n    for (const name of valid_classes) {\n      container.classList.toggle(name, name == cl);\n    }\n  }\n  // We use the custom getters we'll set up in the container\n  const { ui_value, config_value, config_span, key } = container;\n  if (config_value === undefined) {\n    setClass(\"missing-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> is not present in the config.`;\n  } else if (ui_value == config_value) {\n    setClass(\"matching-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has the same value in the config and in the header.`;\n  } else {\n    setClass(\"different-config\");\n    config_span.innerHTML = `The key <b><em>\${key}</em></b> has a different value (<em>\${config_value}</em>) in the config.`;\n  }\n  // Add info about setting and unsetting\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click on the label <em><b>once</b></em> to set the current UI value in the config.`\n  );\n  config_span.insertAdjacentHTML(\n    \"beforeend\",\n    `<br>Click <em><b>twice</b></em> to remove this key from the config.`\n  );\n}\n\nconst valid_formats = [\"png\", \"svg\", \"webp\", \"jpeg\", \"full-json\"];\nfunction initializeUIValueSpan(span, key, value) {\n  const container = span.closest(\".clipboard-span\");\n  span.contentEditable = key === \"format\" ? \"false\" : \"true\";\n  let parse = (x) => x;\n  let update = (x) => (span.textContent = x);\n  if (key === \"width\" || key === \"height\") {\n    parse = (x) => Math.round(parseFloat(x));\n  } else if (key === \"scale\") {\n    parse = parseFloat;\n  } else if (key === \"format\") {\n    // We remove contentEditable\n    span.contentEditable = \"false\";\n    // Here we first add the subspans for each option\n    const opts_div = span.appendChild(html`<div class=\"format-options\"></div>`);\n    for (const fmt of valid_formats) {\n      const opt = opts_div.appendChild(\n        html`<span class=\"format-option \${fmt}\">\${fmt}</span>`\n      );\n      opt.onclick = (e) => {\n        span.value = opt.textContent;\n      };\n    }\n    parse = (x) => {\n      return valid_formats.includes(x) ? x : localValue;\n    };\n    update = (x) => {\n      for (const opt of opts_div.children) {\n        opt.classList.toggle(\"selected\", opt.textContent === x);\n      }\n    };\n  } else {\n    // We only have filename here\n  }\n  let localValue;\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return localValue;\n    },\n    set: (val) => {\n      if (val !== \"\") {\n        localValue = parse(val);\n      }\n      update(localValue);\n      checkConfigSync(container);\n    },\n  });\n  // We also assign a listener so that the editable is blurred when enter is pressed\n  span.onkeydown = (e) => {\n    if (e.keyCode === 13) {\n      e.preventDefault();\n      span.blur();\n    }\n  };\n  span.value = value;\n}\n\nfunction initializeConfigValueSpan(span, key) {\n  // Here we mostly want to define the setter and getter\n  const container = span.closest(\".clipboard-span\");\n  Object.defineProperty(span, \"value\", {\n    get: () => {\n      return plot_obj.config.toImageButtonOptions[key];\n    },\n    set: (val) => {\n      // if undefined is passed, we remove the entry from the options\n      if (val === undefined) {\n        delete plot_obj.config.toImageButtonOptions[key];\n      } else {\n        plot_obj.config.toImageButtonOptions[key] = val;\n      }\n      checkConfigSync(container);\n    },\n  });\n}\n\nconst config_spans = {};\nfor (const [key, value] of Object.entries(getImageOptions())) {\n  const container = CLIPBOARD_HEADER.querySelector(`.clipboard-span.\${key}`);\n  const label = container.querySelector(\".label\");\n  // We give the label a function that on single click will set the current value and with double click will unset it\n  label.onclick = DualClick(\n    () => {\n      container.config_value = container.ui_value;\n    },\n    (e) => {\n      console.log(\"e\", e);\n      e.preventDefault();\n      container.config_value = undefined;\n    }\n  );\n  const ui_value_span = container.querySelector(\".clipboard-value\");\n  const config_value_span =\n    container.querySelector(\".config-value\") ??\n    label.insertAdjacentElement(\n      \"afterbegin\",\n      html`<span class=\"config-value\"></span>`\n    );\n  // Assing the two spans as properties of the containing span\n  container.ui_span = ui_value_span;\n  container.config_span = config_value_span;\n  container.key = key;\n  config_spans[key] = container;\n  if (firstRun) {\n    plot_obj.config.toImageButtonOptions =\n      plot_obj.config.toImageButtonOptions ?? {};\n    // We do the initialization of the value span\n    initializeUIValueSpan(ui_value_span, key, value);\n    // Then we initialize the config value\n    initializeConfigValueSpan(config_value_span, key);\n    // We put some convenience getters/setters\n    // ui_value forward\n    Object.defineProperty(container, \"ui_value\", {\n      get: () => ui_value_span.value,\n      set: (val) => {\n        ui_value_span.value = val;\n      },\n    });\n    // config_value forward\n    Object.defineProperty(container, \"config_value\", {\n      get: () => config_value_span.value,\n      set: (val) => {\n        config_value_span.value = val;\n      },\n    });\n  }\n}\n\n// These objects will contain the default value\n\n// This code updates the image options in the PLOT config with the provided ones\nfunction setImageOptions(o) {\n  for (const [key, container] of Object.entries(config_spans)) {\n    container.config_value = o[key];\n  }\n}\nfunction unsetImageOptions() {\n  setImageOptions({});\n}\n\nconst set_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.set\");\nconst unset_button = CLIPBOARD_HEADER.querySelector(\".clipboard-span.unset\");\nif (firstRun) {\n  set_button.onclick = (e) => {\n    for (const container of Object.values(config_spans)) {\n      container.config_value = container.ui_value;\n    }\n  };\n  unset_button.onclick = unsetImageOptions;\n}\n\n// We add a function to check if the clipboard is popped out\nCONTAINER.isPoppedOut = () => {\n  return CONTAINER.classList.contains(\"popped-out\");\n};\n\nCLIPBOARD_HEADER.onmousedown = function (event) {\n  if (event.target.matches(\"span.clipboard-value\")) {\n    console.log(\"We don't move!\");\n    return;\n  }\n  const start = {\n    left: parseFloat(CONTAINER.style.left),\n    top: parseFloat(CONTAINER.style.top),\n    X: event.pageX,\n    Y: event.pageY,\n  };\n  function moveAt(event, start) {\n    const top = event.pageY - start.Y + start.top + \"px\";\n    const left = event.pageX - start.X + start.left + \"px\";\n    CLIPBOARD_HEADER.style.left = left;\n    CONTAINER.style.left = left;\n    CONTAINER.style.top = top;\n  }\n\n  // move our absolutely positioned ball under the pointer\n  moveAt(event, start);\n  function onMouseMove(event) {\n    moveAt(event, start);\n  }\n\n  // We use this to remove the mousemove when clicking outside of the container\n  const controller = new AbortController();\n\n  // move the container on mousemove\n  document.addEventListener(\"mousemove\", onMouseMove, {\n    signal: controller.signal,\n  });\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        cleanUp();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n\n  function cleanUp() {\n    console.log(\"cleaning up the plot move listener\");\n    controller.abort();\n    CLIPBOARD_HEADER.onmouseup = null;\n  }\n\n  // (3) drop the ball, remove unneeded handlers\n  CLIPBOARD_HEADER.onmouseup = cleanUp;\n};\n\nfunction sendToClipboard(blob) {\n  if (!navigator.clipboard) {\n    alert(\n      \"The Clipboard API does not seem to be available, make sure the Pluto notebook is being used from either localhost or an https source.\"\n    );\n  }\n  navigator.clipboard\n    .write([\n      new ClipboardItem({\n        // The key is determined dynamically based on the blob's type.\n        [blob.type]: blob,\n      }),\n    ])\n    .then(\n      function () {\n        console.log(\"Async: Copying to clipboard was successful!\");\n      },\n      function (err) {\n        console.error(\"Async: Could not copy text: \", err);\n      }\n    );\n}\n\nfunction copyImageToClipboard() {\n  // We extract the image options from the provided parameters (if they exist)\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key. We also ignore format because the clipboard only supports png.\n    if (val === undefined || key === \"format\") {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.toImage(PLOT, config).then(function (dataUrl) {\n    fetch(dataUrl)\n      .then((res) => res.blob())\n      .then((blob) => {\n        const paste_receiver = document.querySelector('paste-receiver.plutoplotly')\n        if (paste_receiver) {\n          paste_receiver.attachImage(dataUrl, CONTAINER)\n        }\n        sendToClipboard(blob)\n      });\n  });\n}\n\nfunction saveImageToFile() {\n  const config = {};\n  for (const [key, container] of Object.entries(config_spans)) {\n    let val =\n      container.config_value ??\n      (CONTAINER.isPoppedOut() ? container.ui_value : undefined);\n    // If we have undefined we don't create the key.\n    if (val === undefined) {\n      continue;\n    }\n    config[key] = val;\n  }\n  Plotly.downloadImage(PLOT, config);\n}\n\nlet container_rect = { width: 0, height: 0, top: 0, left: 0 };\nfunction unpop_container(cl) {\n  CONTAINER.classList.toggle(\"popped-out\", false);\n  CONTAINER.classList.toggle(cl, false);\n  // We fix the height back to the value it had before popout, also setting the flag to signal that upon first resize we remove the fixed inline-style\n  CONTAINER.style.height = container_rect.height + \"px\";\n  remove_container_size = true;\n  // We set the other fixed inline-styles to null\n  CONTAINER.style.width = \"\";\n  CONTAINER.style.top = \"\";\n  CONTAINER.style.left = \"\";\n  // We also remove the CLIPBOARD_HEADER\n  CLIPBOARD_HEADER.style.width = \"\";\n  CLIPBOARD_HEADER.style.left = \"\";\n  // Finally we remove the hidden class to the header\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", true);\n  return;\n}\nfunction popout_container(opts) {\n  const cl = opts?.cl;\n  const target_container_size = opts?.target_container_size ?? {};\n  const target_plot_size = opts?.target_plot_size ?? {};\n  if (CONTAINER.isPoppedOut()) {\n    return unpop_container(cl);\n  }\n  CONTAINER.classList.toggle(cl, cl === undefined ? false : true);\n  // We extract the current size of the container, save them and fix them\n  const { width, height, top, left } = CONTAINER.getBoundingClientRect();\n  container_rect = { width, height, top, left };\n  // We save the current plot size before we pop as it will fill the screen\n  const current_plot_size = {\n    width: PLOT._fullLayout.width,\n    height: PLOT._fullLayout.height,\n  };\n  // We have to save the pad data before popping so we can resize precisely\n  const pad = {};\n  pad.unpopped = getSizeData().container_pad;\n  CONTAINER.classList.toggle(\"popped-out\", true);\n  pad.popped = getSizeData().container_pad;\n  // We do top and left based on the current rect\n  for (const key of [\"top\", \"left\"]) {\n    const start_val = target_container_size[key] ?? container_rect[key];\n    let offset = 0;\n    for (const kind of [\"padding\", \"border\"]) {\n      offset += pad.popped[kind][key] - pad.unpopped[kind][key];\n    }\n    CONTAINER.style[key] = start_val - offset + \"px\";\n    if (key === \"left\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  // We compute the width and height depending on eventual config data\n  const csz = computeContainerSize({\n    width:\n      target_plot_size.width ??\n      config_spans.width.config_value ??\n      current_plot_size.width,\n    height:\n      target_plot_size.height ??\n      config_spans.height.config_value ??\n      current_plot_size.height,\n  });\n  for (const key of [\"width\", \"height\"]) {\n    const val = target_container_size[key] ?? csz[key];\n    CONTAINER.style[key] = val + \"px\";\n    if (key === \"width\") {\n      CLIPBOARD_HEADER.style[key] = CONTAINER.style[key];\n    }\n  }\n  CLIPBOARD_HEADER.classList.toggle(\"hidden\", false);\n  const controller = new AbortController();\n\n  document.addEventListener(\n    \"mousedown\",\n    (e) => {\n      if (e.target.closest(\".plutoplotly-container\") !== CONTAINER) {\n        unpop_container();\n        controller.abort();\n        return;\n      }\n    },\n    { signal: controller.signal }\n  );\n}\n\nCONTAINER.popOut = popout_container;\n\nfunction DualClick(single_func, dbl_func) {\n  let nclicks = 0;\n  return function (...args) {\n    nclicks += 1;\n    if (nclicks > 1) {\n      dbl_func(...args);\n      nclicks = 0;\n    } else {\n      delay(300).then(() => {\n        if (nclicks == 1) {\n          single_func(...args);\n        }\n        nclicks = 0;\n      });\n    }\n  };\n}\n\n// We remove the default download image button\nplot_obj.config.modeBarButtonsToRemove = _.union(\n  plot_obj.config.modeBarButtonsToRemove,\n  [\"toImage\"]\n);\n// We add the custom button to the modebar\nplot_obj.config.modeBarButtonsToAdd = _.union(\n  plot_obj.config.modeBarButtonsToAdd,\n  [\n    {\n      name: \"Copy PNG to Clipboard\",\n      icon: {\n        height: 520,\n        width: 520,\n        path: \"M280 64h40c35.3 0 64 28.7 64 64V448c0 35.3-28.7 64-64 64H64c-35.3 0-64-28.7-64-64V128C0 92.7 28.7 64 64 64h40 9.6C121 27.5 153.3 0 192 0s71 27.5 78.4 64H280zM64 112c-8.8 0-16 7.2-16 16V448c0 8.8 7.2 16 16 16H320c8.8 0 16-7.2 16-16V128c0-8.8-7.2-16-16-16H304v24c0 13.3-10.7 24-24 24H192 104c-13.3 0-24-10.7-24-24V112H64zm128-8a24 24 0 1 0 0-48 24 24 0 1 0 0 48z\",\n      },\n      direction: \"up\",\n      click: DualClick(copyImageToClipboard, () => {\n        popout_container();\n      }),\n    },\n    {\n      name: \"Download Image\",\n      icon: Plotly.Icons.camera,\n      direction: \"up\",\n      click: DualClick(saveImageToFile, () => {\n        popout_container({ cl: \"filesave\" });\n      }),\n    },\n  ]\n);\n"), HypertextLiteral.JavaScript("function getOffsetData(el) {\n  let cs = window.getComputedStyle(el, null);\n  const odata = {\n    padding: {\n      left: parseFloat(cs.paddingLeft),\n      right: parseFloat(cs.paddingRight),\n      top: parseFloat(cs.paddingTop),\n      bottom: parseFloat(cs.paddingBottom),\n      width: parseFloat(cs.paddingLeft) + parseFloat(cs.paddingRight),\n      height: parseFloat(cs.paddingTop) + parseFloat(cs.paddingBottom),\n    },\n    border: {\n      left: parseFloat(cs.borderLeftWidth),\n      right: parseFloat(cs.borderRightWidth),\n      top: parseFloat(cs.borderTopWidth),\n      bottom: parseFloat(cs.borderBottomWidth),\n      width: parseFloat(cs.borderLeftWidth) + parseFloat(cs.borderRightWidth),\n      height: parseFloat(cs.borderTopWidth) + parseFloat(cs.borderBottomWidth),\n    }\n  };\n  if (el === PLOT) {\n    // For the PLOT we also want to take into account the offset\n    odata.offset = {\n      top: PLOT.offsetParent == CONTAINER ? PLOT.offsetTop : 0,\n      left: PLOT.offsetParent == CONTAINER ? PLOT.offsetLeft : 0,\n    }\n  }\n  return odata;\n}\nfunction getSizeData() {\n  const data = {\n    plot_pad: getOffsetData(PLOT),\n    plot_rect: PLOT.getBoundingClientRect(),\n    container_pad: getOffsetData(CONTAINER),\n    container_rect: CONTAINER.getBoundingClientRect(),\n  };\n  return data;\n}\nfunction computeContainerSize({ width, height }, sizeData = getSizeData()) {\n  const computed_size = computePlotSize(sizeData);\n  const offsets = computed_size.offsets;\n\n  const plot_data = {\n    width: width ?? computed_size.width,\n    height: height ?? computed_size.height,\n  };\n\n  return {\n    width: (width ?? computed_size.width) + offsets.width,\n    height: (height ?? computed_size.height) + offsets.height,\n    noChange: width == computed_size.width && height == computed_size.height,\n  }\n}\n\n// This function will change the container size so that the resulting plot will be matching the provided specs\nfunction changeContainerSize({ width, height }, sizeData = getSizeData()) {\n  if (!CONTAINER.isPoppedOut()) {\n    console.log(\"Tried to change container size when not popped, ignoring\");\n    return;\n  }\n\n  const csz = computeContainerSize({ width, height }, sizeData);\n\n  if (csz.noChange) {\n    console.log(\"Size is the same as current, ignoring\");\n    return\n  }\n  // We are now going to set he width and height of the container\n  for (const key of [\"width\", \"height\"]) {\n    CONTAINER.style[key] = csz[key] + \"px\";\n  }\n}\n// We now create the function that will update the plot based on the values specified\nfunction updateFromHeader() {\n  const header_data = {\n    height: config_spans.height.ui_value,\n    width: config_spans.width.ui_value,\n  };\n  changeContainerSize(header_data);\n}\n// We assign this function to the onblur event of width and height\nif (firstRun) {\n  for (const container of Object.values(config_spans)) {\n    container.ui_span.onblur = (e) => {\n      container.ui_value = container.ui_span.textContent;\n      updateFromHeader();\n    };\n  }\n}\n// This function computes the plot size to use for relayout as a function of the container size\nfunction computePlotSize(data = getSizeData()) {\n  // Remove Padding\n  const { container_pad, plot_pad, container_rect } = data;\n  const offsets = {\n    width:\n      plot_pad.padding.width +\n      plot_pad.border.width +\n      plot_pad.offset.left +\n      container_pad.padding.width +\n      container_pad.border.width,\n    height:\n      plot_pad.padding.height +\n      plot_pad.border.height +\n      plot_pad.offset.top +\n      container_pad.padding.height +\n      container_pad.border.height,\n  };\n  const sz = {\n    width: Math.round(container_rect.width - offsets.width),\n    height: Math.round(container_rect.height - offsets.height),\n    offsets,\n  };\n  return sz;\n}\n\n// Create the resizeObserver to make the plot even more responsive! :magic:\nconst resizeObserver = new ResizeObserver((entries) => {\n  const sizeData = getSizeData();\n  const {container_rect, container_pad} = sizeData;\n  let plot_size = computePlotSize(sizeData);\n  // We save the height in the PLOT object\n  PLOT.container_height = container_rect.height;\n  // We deal with some stuff if the container is poppped\n  CLIPBOARD_HEADER.style.width = container_rect.width + \"px\";\n  CLIPBOARD_HEADER.style.left = container_rect.left + \"px\";\n  config_spans.height.ui_value = plot_size.height;\n  config_spans.width.ui_value = plot_size.width;\n  /* \n\t\tThe addition of the invalid argument `plutoresize` seems to fix the problem with calling `relayout` simply with `{autosize: true}` as update breaking mouse relayout events tracking. \n\t\tSee https://github.com/plotly/plotly.js/issues/6156 for details\n\t\t*/\n  let config = {\n    // If this is popped out, we ignore the original width/height\n    width: (CONTAINER.isPoppedOut() ? undefined : original_width) ?? plot_size.width,\n    height: (CONTAINER.isPoppedOut() ? undefined : original_height) ?? plot_size.height,\n    plutoresize: true,\n  };\n  Plotly.relayout(PLOT, config).then(() => {\n    if (remove_container_size && !CONTAINER.isPoppedOut()) {\n      // This is needed to avoid the first resize upon plot creation to already be without a fixed height\n      CONTAINER.style.height = \"\";\n      CONTAINER.style.width = \"\";\n      remove_container_size = false;\n    }\n  });\n});\n\nresizeObserver.observe(CONTAINER);\n"), HypertextLiteral.JavaScript("\nPlotly.react(PLOT, plot_obj).then(() => {\n\t// Assign the Plotly event listeners\n\tfor (const [key, listener_vec] of Object.entries(plotly_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.on(key, listener)\n\t\t}\n\t}\n\t// Assign the JS event listeners\n\tfor (const [key, listener_vec] of Object.entries(js_listeners)) {\n\t\tfor (const listener of listener_vec) {\n\t\t\tPLOT.addEventListener(key, listener, {\n\t\t\t\tsignal: controller.signal\n\t\t\t})\n\t\t}\n\t}\n}\n)\n"), HypertextLiteral.JavaScript("\ninvalidation.then(() => {\n\t// Remove all plotly listeners\n\tPLOT.removeAllListeners()\n\t// Remove all JS listeners\n\tcontroller.abort()\n\t// Remove the resizeObserver\n\tresizeObserver.disconnect()\n})\n")])), nothing, nothing, nothing, nothing)

Problema 8.19

Sea un proceso cuya función de transferencias es:

\[G_p = \frac{10 \mathrm{e}^{- 0.1 s}}{0.5 s + 1}\]

Los valores de los parámetros se han determinado con un error de ±20 %. Calcular la mayor ganancia de un controlador proporcional que hace al ciclo cerrado estable. Suponer \(G_m = G_f = 1\).